Пошаговое объяснение:1) Если поделить поделить 123456 на 248 то целая часть числа составит 497, это нкикак не приблизительно 5000
1. Иногда верное, иногда нет:100000/100=1000, а 100000/500=200
2.Никогда не верно, ведь нечетное число всегда дает остаток приделение на 2 равный единице => что такое число не может нацело
делиться на 2
3.Да, это всегда верно.Можно обьяснить это как признак делимости на 100, или или то что это сичло имеет вид abc00, которое раскладывается как 10000a+1000b+100c+0+0, можно заметить, что каждый из множителей делится на 100
Свойства квадратных корней, которыми воспользуемся:
1)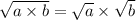 ;
;
2)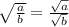 ;
;
3)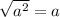 .
.
Итак, для начала нужно разложить числа под корнем на множители. Причём на такие множители, которые являются квадратом какого-то числа, чтобы можно было воспользоваться третьим свойством корней и вынести из под знака корня это какое-то число, тем самым упростить.
1)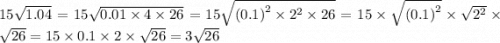 ;
;
2)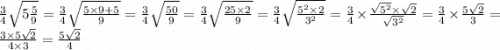 ;
;
3)
для удобства дальнейшего решения избавимся от иррациональности в знаменателе, то есть, от знака корня в знаменателе
4) ;
;
5)
Теперь объединяем это всё:
Сгруппируем числа с разными корнями: