Дано уравнение x² + (2a - 3)x + 3a² - 2a = 0.
Чтобы квадратное уравнение имело 2 корня, надо, чтобы его дискриминант был больше 0.
Находим дискриминант:
D = (2a - 3)² - 4*1*(3a² - 2a) = 4a² - 12a + 9 - 12a² + 8a = -8a² - 4a + 9.
Приравниваем нулю: -8a² - 4a + 9 = 0. D = 16 + 288 = 304. √304 = 4√19. a1 = (4 - 4√19)/(-16) = (1 - √19)/(-4) ≈ 0,84.
a2 = (4 + 4√19)/(-16) = (1 + √19)/(-4) ≈ -1,34.
Для квадратного уравнения с отрицательным коэффициентом при х² положительные корни а находятся между -1,34 и 0,84.
Далее, отрицательные корни заданного уравнения могут быть при положительном значении коэффициента при х (то есть ось параболы должна быть сдвинута влево): 2а - 3 > 0, a > 3/2.
Это противоречит первому условию.
ответ: задача не имеет решения.
Найдем интеграл от f(x)
Получаем:
Надо найти C.
Известно что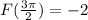
Подставим в найденное F(x), получим:
Получили, что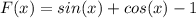
Дальше надо решить уравнение:
Итак получили 2 решения, теперь обратим внимание на условие:![f: [\pi;2\pi] \to R](/tpl/images/0070/1780/e655c.png) , что под ним подразумевалось изначально, я не уверен, может быть этим условием хотели сказать что нас интересуют только действительные корни уравнения и мы не рассматриваем пространство комплексных корней, но скорее всего здесь это было сделано для того чтобы ограничить область в которой лежат нули первообразной, областью следующего вида:
, что под ним подразумевалось изначально, я не уверен, может быть этим условием хотели сказать что нас интересуют только действительные корни уравнения и мы не рассматриваем пространство комплексных корней, но скорее всего здесь это было сделано для того чтобы ограничить область в которой лежат нули первообразной, областью следующего вида: ![x \in [\pi; 2\pi]](/tpl/images/0070/1780/72d02.png) . Будем полагать что это так, тогда нули первообразной
. Будем полагать что это так, тогда нули первообразной 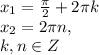 лежат на данном отрезке при n=1, и первый корень вообще не будет лежать на отрезке при любых значениях k
лежат на данном отрезке при n=1, и первый корень вообще не будет лежать на отрезке при любых значениях k
таким образом получается, что:
Подводя итог получаем
Нулями производной будут: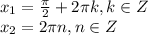
Однако условию![f: [\pi;2\pi] \to R](/tpl/images/0070/1780/e655c.png) удовлетворяет только
удовлетворяет только 
ответ: