Максимальное количество оказывается в ряде 2,...,11. Это 2,3,5,7,11, то есть 5.
В ряде 3,...,12 это 3,5,7,11, то есть 4.
В ряде 6,...,15 это 7,11,13, то есть 3.
В ряде 20,...,29 это 23,29, то есть 2.
В ряде 90,...,99 это 97, то есть 1.
В ряде 200,..,209 простых чисел нет, то есть 0.
ответ: в ряде из 10 последовательных натуральных чисел может быть от 0 до 5 (включительно) простых чисел.
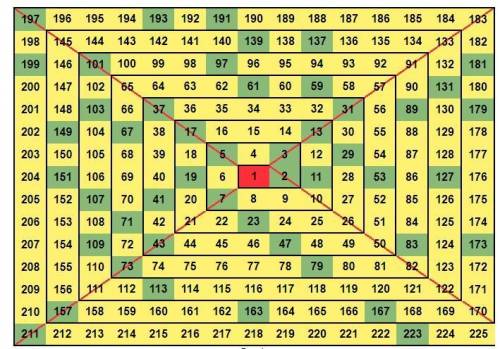
Картинка с числами до 225 приложена. В ней зеленым отмечены простые числа. (1, кстати, не является простым числом, она красным отмечена)
№1
5 \frac{7}{8}+2 \frac{5}{12}=5 \frac{7*3}{24}+2 \frac{5*2}{24} =5 \frac{21}{24}+2 \frac{10}{24}=7 \frac{31}{24} =8 \frac{7}{24}5
8
7
+2
12
5
=5
24
7∗3
+2
24
5∗2
=5
24
21
+2
24
10
=7
24
31
=8
24
7
1 \frac{1}{9} +2 \frac{3}{5} =1 \frac{1*5}{45} +2 \frac{5*3}{45}=3 \frac{20}{45}= 3\frac{4}{9}1
9
1
+2
5
3
=1
45
1∗5
+2
45
5∗3
=3
45
20
=3
9
4
8 \frac{3}{5}+ \frac{1}{15}=8\frac{3*3}{15}+ \frac{1}{15}= 8 \frac{10}{15}= 8 \frac{2}{3}8
5
3
+
15
1
=8
15
3∗3
+
15
1
=8
15
10
=8
3
2
\frac{2}{3}+4 \frac{3}{5}= \frac{2*5}{15}+4 \frac{3*3}{15}=4 \frac{19}{15}=5 \frac{4}{15}
3
2
+4
5
3
=
15
2∗5
+4
15
3∗3
=4
15
19
=5
15
4
№2
2- \frac{5}{6}=1 \frac{6}{6}-\frac{5}{6}=1 \frac{1}{6}2−
6
5
=1
6
6
−
6
5
=1
6
1
6-5 \frac{5}{8}=5\frac{8}{8}-5\frac{5}{8}=\frac{3}{8}6−5
8
5
=5
8
8
−5
8
5
=
8
3
3,4 пример на картинке.
№3
x + 2\frac{2}{11} =5x+2
11
2
=5
x=5-2 2/11
x=4 11/11-2 2/11
x=2 9/11