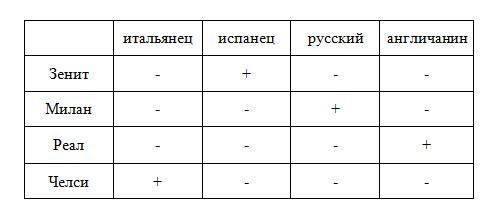
Так как национальность тренеров не совпадала с национальностью команд, то ставим прочерки в таблице в соответствующих клетках.
"Зенит" не тренируется у Джона и Антонио, значит, тренер "Зенита" - испанец Родриго. Ставим в таблице "плюс" и остальные по вертикали - "минус".
Тренер "Милана" - не англичанин и, так как у "Милана" остается только одна свободная клетка, то тренер этой команды - русский. Ставим "плюс" и остальные по вертикали - "минус".
В строчке с "Челси" осталась одна свободная клетка. Значит тренер этой команды - итальянец, а тренер "Реала" - англичанин.
ответ: команду России тренирует испанец Родриго, команду Италии - русский Николай, команду Англии - итальянец Антонио, команду Испании - англичанин Джон.
1; 2; 3; 4; ...; Х
Сумма ряда находится по ф-ле: S = (1 + N)*N/2, по условию она 100 книг, а N у нас Х, т.е.
(1+Х)*Х/2 = 100; ⇒ Х + Х² = 200 или
Х² + Х - 200 = 0; D = 1+4*200=801; D>0;
Х₁ = (-1 + √D) / 2 = (-1 + √801) / 2 ≈ (-1 + 28,3) / 2 ≈ 27,3 / 2 ≈ 13,7
Х₂ = (-1 - √D) / 2 = -14,7
Так как Х - число школьников,то оно должно быть положительным и целым. Т.е Х = 13
ответ: Б) 13 школьников максимально могут получить разное количество книг, если их распределяется 100.
Проверка:
Мы распределим (1+13)*13/2 = 91 книг, останется 100 - 91 = 9 книг. Их уже нельзя дать 14-ому школьнику, так как 9 книг уже получено девятым. (Остаток можно распределять последним по счету).