3 км/ч - скорость пешком, 12 км/ч - скорость на велосипеде
Пошаговое объяснение:
Пусть x - скорость туриста пешком, y - скорость туриста на велосипеде.
Составляем систему уравнений:
2x+y=20
x+2y=28
Решаем методом сложения:
2x+y=20 /*2
x+2y=28
4x+2y=40
x+2y=28 вычитаем => 3x=12; x=3 км/ч - скорость пешком
y=20-2*3=12 км/ч - скорость на велосипеде
Пошаговое объяснение:
\ begin {gather} sin \ 2x + sin \ 6x = 0 \\ 2sin \ frac {2x + 6x} {2} cos \ frac {2x-6x} {2} = 0 \\ sin \ 4x \ cos \ 2x = 0 \\ \ left [{{sin \ 4x = O} \ atop {cos \ 2x = 0}} \ right. <=> \ left [{{4x = \ pi k} \ atop {2x = \ frac {\ pi} {2} +2 \ pi n}} \ right. <=> \ left [{{x = \ frac {\ pi k} {4} \ atop {x = \ frac {\ pi} {4} + \ pi n}} \ right. => x = \ dfrac {\ pi m} {4} \\ k \ in Z, \ n \ in Z, \ m \ in Z. \ ||| Ombem: \ \ \ dfrac {\ pi m} {4}; \ \ m \ in Z. \ end {gather}% 3D
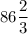
Пошаговое объяснение:
Чтобы найти часть (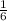 
) числа (120), выраженную дробью, надо это число (120) умножить на дробь:
1) 
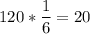(кг) картофеля израсходовали в первый день.
Узнаем, сколько кг картофеля осталось после того, как часть израсходовали в первый день, путем вычитания из исходного количества картофеля части, которую израсходовали в первый день:
2) 120-20 = 100 (кг) картофеля осталось после первого дня.
Узнаем, сколько израсходовали во второй день. Для этого нужно найти часть (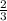 
) от остатка (100):
3) 
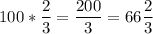(кг) картофеля израсходовали во второй день.
Сложим израсходованное количество картофеля в первый и во второй день, для нахождения количества, которое израсходовали за 2 дня вместе:
4) 
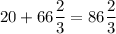(кг) картофеля израсходовали за два дня.
Відповідь:
Покрокове пояснення:
Нехай х швидкість пішки та у -велосипедом
Тоді можна скласти систему:
2х+у=20
х+2у=28
з першого у=20-2х і підставимо в друге
х+40-4х=28
3х=12
х=4 → у=12
швидкість туриста пішки 4км/год та на велосипеді 12км/год