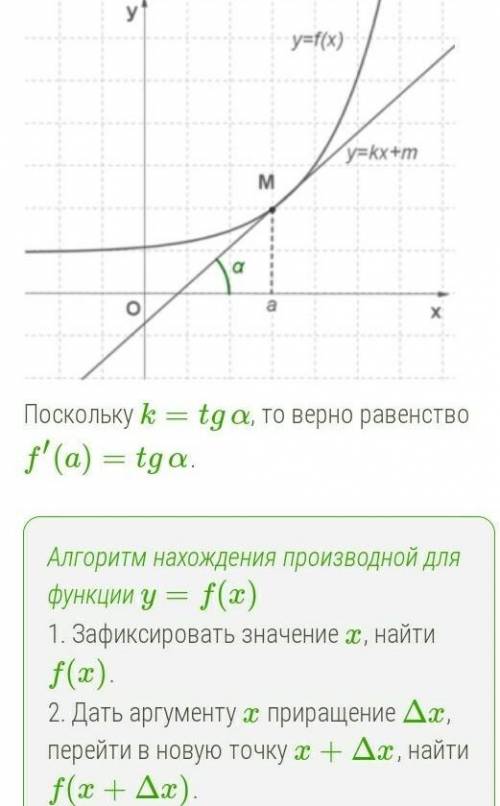
все в картинках........-----
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные - машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению - промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.

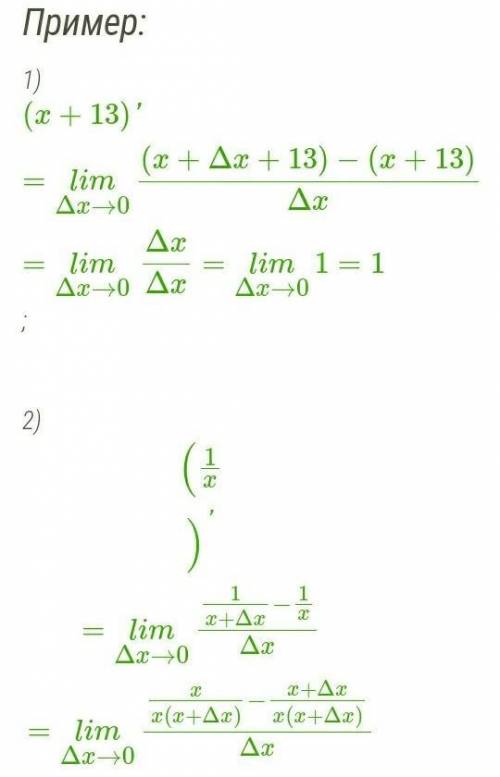


через 5 минут
Пошаговое объяснение:
Когда Витя спохватился, между ними было 20 минут хода. так как Витя ускорился в 5 раз, эти 20 минут он преодолеет за 4 минуты. За эти 4 минуты мама соответственно тоже некоторое расстояние, поэтому Вите вновь придется ее догонять.
Пусть скорость мамы х, тогда скорость Вити 5х
Их скорость сближения 5х-х=4х
разница между ними во времени:4 минуты
4х=4
х=1
через минуту он догонит маму
итого получается что на все у него уйдет 5 минут.
Можно изначально было записать, что так как скорость сближения у них 4х, а разница во времени 20 минут, то 4х=20, откуда х=5.