
ответ:
Пошаговое объяснение:
Заданы формулы для правильного многоугольника.
В нашем случае правильного четырехугольника или квадрата.
Заданы формулы:
Длина многоугольника через радиус описанной окружности
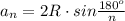
Для квадрата
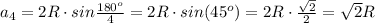
или
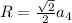
Радиус вписанной окружности через радиус описанной окружности
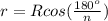
Для квадрата
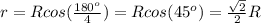
или
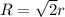
Площадь многоугольника через периметр и радиус вписанной окружности
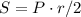 или
или 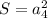
Определим значения первой строки таблицы зная, что сторона квадрата a = 6.
Радиус описанной окружности
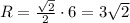
Радиус вписанной окружности
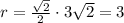
Периметр

Площадь квадрата

или 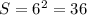
Определим значения второй строки таблицы зная, что радиус вписанной окружности r=2.
Радиус описанной окружности
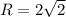
Длина стороны квадрата
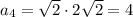
или

Периметр

Площадь квадрата

Определим значения третьей строки таблицы зная, что радиус описанyой окружности R=4.
Длина стороны квадрата
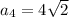
Радиус вписанной окружности
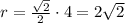
Периметр
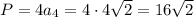
Площадь квадрата
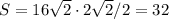
Определим значения четвертой строки таблицы зная, что периметр квадрата P=28.
Длина стороны квадрата
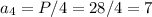
Радиус описанной окружности
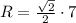
Радиус вписанной окружности
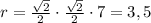
Площадь квадрата
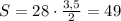
Определим значения пятой строки таблицы зная, что площадь квадрата S=16.
Длина стороны квадрата
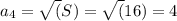
Далее как для второй строки.
Повторять не буду
Подставим значения в таблицу

1. Реши задачу
Из двух городов одновременно навстречу друг другу отправились скорый и товарный
поезда. Они встретились через 8 ч. Каково расстояние между городами, если известно, что
скорость скорого поезда 120 км/ч, а скорость товарного поезда составляет половину сут
скорости скорого поезда?
2. Вычисли значение выражений
815 204 - (8 963 - 68 077): 36
9676 + 12. 237 - 8 787 2:29
5 400 кг 54 ц
3. Сравни величины
4 ч 20 мин. на
420 мин
970 см 97 м
3 дм? 7 см. 307 см
4. Рении уравнение Х- 807 = 140: 2
5. Реши задачу. Длина огорода прямоугольной формы 20м, а ширина н2раза меньше
Сколько метров сетки потребуется, чтобы огородить его со всех сторон? Найди площадь
этого огорода.
1) Найдём точки пересечения графиков:
y = 0.5x² ; y = 4-x
0.5x² = 4-x
x²+2x - 8 = 0
x = -4;
x = 2;
Построим графики двух функций (фото №1)
функция y = 4-x располагается выше y = 0.5x²,
по-этому площадь фигуры считается как :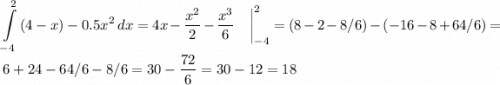
ответ: площадь равна 18 квадратных единиц