До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Цель: 1) Рабит Батулла “Чикыл Мырый с” сказка литературе; 2) Развитие речи учащихся, связанный языка; правильно отвечать на вопросы изучения; 3) воспитание нравственности у учащихся качества. Оборудование: проектор, карточки, рисунки, куклы. Тип урока: урок смешанный План урока. Часть I. организации. Поздороваться. Добрый день, ребята! Давайте познакомимся! Меня зовут - Гульназ Фәридовна. Как вас ваше имя? Я вижу-вижу имя. Я рада, что познакомилась с вами. А сейчас начинаем урок. II. Актуализации. 1)-ребята, вы посмотреть телевизор ко мне. А канал ТНВ знаете? Какие передачи для детей оказывают на канале ТНВ? “Гостинец передачу” вы видели? (слайд) -А что такое гостинец? (гостинец). Гостинец что показали в передаче? Я сегодня принесла я вам в подарок сказка. А кто пишет сказки? Каких писателей вы знаете? -Ребята, это кто? (слайд) а кто такой Рабит Батулла? Рабит Батулла – сказки > Он очень любит детей. Его сказки дети с удовольствием учатся. -Школьники, Рабит Батулла какие сказки вы знаете? (слайд) 2) сегодня мы с вами Рабит Батулла “Чикыл с Мырый сказки”, сказки же изучим выделены по ответить. Давайте в ходу в зависимости от сказки. (Театр кукол) III. Основная часть. 1)слова работа (упражнения фонетик) А сейчас познакомимся с новыми словами. (слайд) я читаю, вы тынла см.
детей мышь-мышонок упал-упал издание мостик не умеет плавать-не умеет плавать яр-берег только родители мечетей и утонул жди меня-учитывая, что хвост-хвост весь жизненный путь-протянул река-река держаться-зацепился это женщины-убежал -Давайте-ка, попробуем эти слова с предложения строительства. 2) ребята, сейчас я читаю сказки, а вы внимательно слушайте.(читаю) Давайте попробуем ответить на вопросы. -Кто выходит из издания? (слайд) Внезапно он сделал? -Городской набережной, кто придет? -Чикыл что кричала? -Что Мырый что? - Мырый сделал? -Чикыл сделал? IV. Окрепли. 1) -ребята, вы понимание содержания сказки вы тоже принимали? Содержание сказка старой понял? Давайте попробуем еще рассказывать. (слайд) - Как вы считаете, правда детей Чикыл работы мыши? А почему решили Мырый Чикыл их заслушивание ответов учащихся) 2) -смотрим на доске. Будем повторять. (Чикыл Мырый размещаются с рисунка на доске, карточки посередине . А читая перевод сәзләр карты принимают) Слов: это женщины – убежал отдых – обманул
смогу закрепиться – хотел съесть А теперь скажите, кто из них Чикыл в эти слова, кто из них Мырый? Хитрость с целью выживания Чикыл девчат. А хитрость с целью питания Мырый девчат. Чикыл солгала ради своего Ради своего Мырый такой цели, а цель была-съесть мышонка. V. Итог Урока. -Хорошо. Вот и наш урок близится к концу. Ребята, мы сегодня на уроке мы что? Название сказки? “С Чикыл Мырый сказки” кто написал? Рабит Батулла кто он? Вы смогли у вас какие новости? (Чикыл как может быть иногда, а не быть как Мырый нельзя) какие слова вы узнали нового? Оставьте запись домашнего задания. 1 учить новые слова. Роль сказки научить читать к 2 отделения. -Давайте-ка, мы попробуем играть сказки с целью облегчения домашнего задания. Сегодня на уроке Вы активное участие Ваш правильный ответ с меня подаренную радость. Если вы мне такой понравился, поэтому я работаю только пятерки, что я хотел. Установке знаков. - Тем самым наш урок завершен, до свидания
7.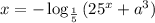
Пусть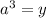 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию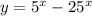 :
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно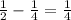 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,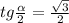
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем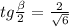
ответ: 4 : 3