1) Найдем скорость догона поездов (то есть скорость первого поезда + скорость второго поезда)
S : t = V
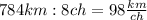 - скорость догона.
- скорость догона.
2) Пусть х км/ч скорость первого поезда, тогда скорость второго поезда (х + 10) км/ч. Т.к скорость догона (то есть сумма их скоростей) равна 98 км/ч, то составляем такое уравнение:
х + (х + 10) = 98
2х = 88
х = 44
ответ х = 44
44 км/ч - скорость первого поезда
3) 44 + 10 = 54 (км/ч) - второго.
ответ: скорость первого поезда 44 км/ч
скорость второго поезда 54 км/ч.
1 км/ч
Пошаговое объяснение:
64/8=8 км/ч - скорость движения лодки по течению
12/2=6 км/ч - скорость движения лодки против течения
x - скорость течения реки.
Для того, чтобы найти собственную скорость лодки (без учета течения), мы, соответственно, если известная скорость по течению, то мы вычитаем его, т.е. 8-x; А если против течения, то мы прибавляем его, т.е. 6+x. Т.к. оба выражения характеризуют скорость движения лодки без учета течения, то мы их можем приравнять:
8-x=6+x
Теперь просто решаем уравнение, перенеся -x в правую часть с противоположным знаком, а 6 в левую с противоп. знаком, получим:
8-6=x+x
2=2x
x=1
Тогда скорость течения равна 1 км/ч