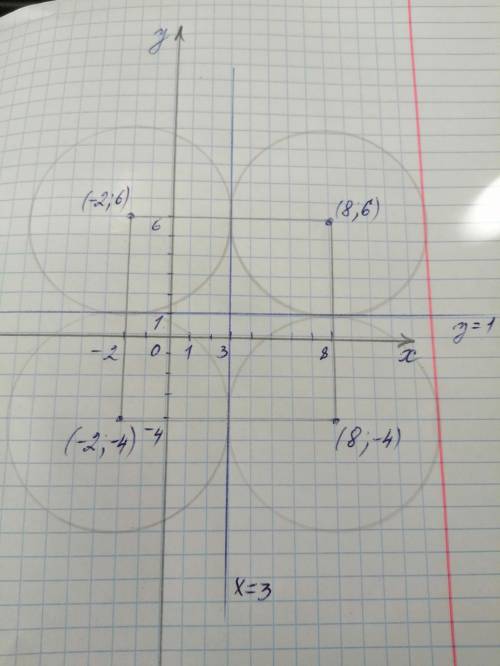
(8;6), (8;-4), (-2;6) и (-2;-4)
Пошаговое объяснение:
(x-x₀)²+(y-y₀)²=25 - уравнение окружности
(x-x₀)²+(y-y₀)²= 5²
R=5 - радиус окружности
Находим координаты центра окружности, если прямые х=3 и у=1 являются касательными к окружности.
Рассмотрим рисунок (в приложении). На нём система координат Оху, прямые х=3 и у=1. На рисунке показано, что окружностей, которые могут касаться данных прямых на самом деле 4. Учитывая, что радиус окружности равен 5, находим координаты центров этих окружностей.
Касательные х=3 и у=1 пересекаются в точке (3;1). От этой точки вправо, влево, вверх и вниз отсчитываем по 5 единиц.
3+5=8
3-5=-2
1+5=6
1-5=-4
Получаем точки (8;6), (8;-4), (-2;6) и (-2;-4), которые и являются центрами окружностей.
a) х = √3 см, у = 2√3 см, или CB = √3 см, AB = 2√3 см.
b) х = 4√2 см, у = 4√2 см, или NM = 4√2 см, NK = 4√2 см.
c) х = 20 см, у = 10√3 см, или PT = 20 см, RT = 10√3 см.
d) х = 2√3 см, у = 4√3/3 см, или EH = 2√3 см, FG = 4√3/3 см.
Пошаговое объяснение:
а) Катет равен другому катету, умноженному на тангенс угла, противолежащего данному катету:
х = 3 * tg 30° = 3 * (√3/3) = √3 см,
у = 2х = 2√3 см, т.к. катет, лежащий против угла 30°, равен половине гипотенузы.
ответ: х = √3 см, у = 2√3 см, или CB = √3 см, AB = 2√3 см.
b)
∠М = 180°-∠N-∠K =180°-90°-45° =45°,
т.к. ∠М = ∠K = 45°, то ΔMNK - равнобедренный и х = у.
Катет равен гипотенузе, умноженной на синус угла противолежащего этому катету:
х = 8*sin45° = 8 * (√2/2) = 4√2
ответ: х = 4√2 см, у = 4√2 см, или NM = 4√2 см, NK = 4√2 см
c)
∠Т = 180°-∠R-∠P = 180°-90°-60° =30°,
PR = 10 cм и лежит против угла в 30°, значит он равен 1/2 гипотенузы х, откуда х = 10* 2 = 20 см;
Катет равен гипотенузе, умноженной на синус угла противолежащего этому катету:
у = 20 * sin60° = 20 * (√3/2) = 10√3 см.
ответ: х = 20 см, у = 10√3 см, или PT = 20 см, RT = 10√3 см
d)
В прямоугольном ΔEFH катет FH лежит против угла 30°, следовательно, гипотенуза EF этого треугольника равна 2FH :
EF = 2* FH = 2* 2 = 4 см;
отсюда х = √(EF²- FH²) = √(4²- 2²) = √(16 -4) = √12 = 2√3.
В прямоугольном ΔFGH катет GH равен другому катету FH, умноженному на тангенс угла, противолежащего этому катету (а угол HFG = 30°):
GH = FH *tg 30° = 2 * (√3/3) = (2√3)/3 см;
отсюда
у = √(FH²+HG²) = √(2²+(2√3/3)²) = √(4 + 4*3/9) = √(36+12)/9= √48/9= √(16*3) /9= 4√3/3 см
ответ: х = 2√3 см, у = 4√3/3 см, или EH = 2√3 см, FG = 4√3/3 см
1) 2
2) не совсем поняла какая именно точка, если самая первая, то ответ 0
3) 4.9x-5.2=0.68
4.9х=0.68+5.2
4.9х=5.88
х=1.2
ответ 1
5) не знаю..
6)1
7)1
8)3
9)2.4а+0.65а-1.05а+12.4=2а+12.4
ответ:1
10)
11)16