Пошаговое объяснение:
Рисунок с графиком в приложении.
Решаем квадратное уравнение.
D = b² - 4*a*c = (2)² - 4*(1)*(0) = 4 - дискриминант. √D = 2.
x₁ = (-b+√D)/(2*a) = (-2+2)/(2*1) = 0 - первый корень
x₂ = (-b-√D)/(2*a) = (-2-2)/(2*1) = -4/2 = -2 - второй корень
1) Нули функции: Х₁ = 0 и Х₂ = -2 - корни уравнения.
2) Минимум функции через первую производную.
y'(x) = 2*x + 2 = 0 и х = -1 - корень производной
3) Экстремум функции: Ymin(-1) = -1.
4) Отрицательна: y<0 x∈(-1;0)
Положительна: y≥0 x∈[-4;-1]∪(0;4]
5) Пересечение с осью ОХ - нули функции - п.6.
6) Пересечение с осью ОУ. у(0) = 0

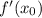
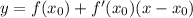

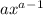 - где а- степень
- где а- степень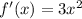 - вот такая вот производная
- вот такая вот производная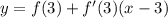
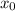 :
: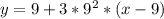
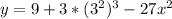
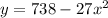
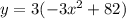 - это и есть касательная в ДАННОЙ точке.
- это и есть касательная в ДАННОЙ точке.
Пусть числа будут х и у. ⇒
x+y=110 y=110-x y=110-x y=110-x y=110-x y=60
0,6x=0,5y |×10 6x=5y 6y=5*(110-x) 6y=550-5x 11x=550 x=50