8кг весит Оля.
Пошаговое объяснение:
х-Оля
х2-Юра
1,5х2-Витя
5х1,5=60
5х=60:1,5
5х=40
х=40:5
х=8
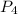= 4! = 24 - возможных перестановок
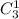= 3 -возможные комбинации
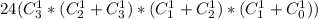= 24 * (3*5*3*1) = 24*45 = 1080 - возможных комбинаций выложить колоду так, чтобы после каждого туза шел король другой масти
Оля весит 10 кг
Пошаговое объяснение: