
ответ:ответ. 102. Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Пошаговое объяснение:
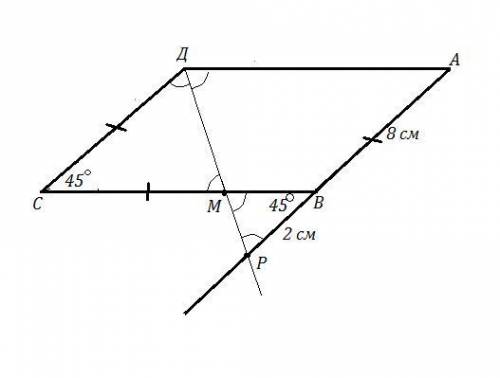
ответ: Р=36 см .
АВСД - параллелограмм , ДР - биссектриса, ∠С=45° ,
ДР пересекает АВ в точке Р , а ВС в точке М .
АР=10 см , ВР=2 см ⇒ АВ=10-2=8 см , СД=АВ=8 см как противоположные стороны параллелограмма .
ДР - биссектриса ⇒ ∠СДР=∠АДР .
∠АДР=∠СМД как накрест лежащие углы при АД || ВС и секущей ДР .
В ΔСМД два угла равны ⇒ ΔСМД - равнобедренный и СМ=СД=8 см ∠СМД=(180°-45°):2=67,5°
∠ВМР=∠СМД=67,5° как вертикальные .
В ΔВМР угол ∠МВР=45° , так как ∠МВР=∠МСД=45° как накрест лежащие углы при АР || СД и секущей ВС .
Но тогда в ΔВМР: ∠ВРМ=180°-45°-67,5°=67,5° , то есть ΔВМР есть два равных угла: ∠ВМР=∠ВРМ=67,5° , тогда этот треугольник равнобедрен-ный и ВМ=ВР=2 см .
Тогда ВС=СМ+ВМ=8 +2 =10 см , АД=ВС=10 см
Периметр Р=10+10+8+8=36 см .
8= 5+8+10+3+7+8+n / 7
n=15
Мода- 8
Медиана- 8