1) Шаровой сегмент – это часть шара, ограниченная секущей плоскостью
2) Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов или вокруг диаметра, не пересекающего его дуги
3) V конуса = ⅓πR²H
4) πR² * H = ⅓πH (4^2 + 4 * 22 + 22^2)
R =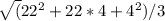
= 14 см
5) V = 4/3πR^3
50 : 2 = 25 см радиус 1 шара, объём V1 = 4/3π25^3.
70 : 2 = 35 см радиус 2 шара, объём V2 = 4/3π35^3.
Найти сумму объёмов V1 + V2 = 4/3π25^3 + 4/3π35^3 = 4/3π (25^3 + 35^3) = 4/3π (15 625 + 42 875) = 4/3π * 58 500 = V3
R = (V3 : 4/3π)1/3 = 58 5001/3 = 38,8
D = 2R = 38,8 * 2 = 77,6 см
6) r = 1/2 * d = 1/2 * 4 = 4/2 = 2 м.
L = √(h2 + r2) = √(3,52 + 22) = √12,25 + 4 = √16,25 = 4,03 м - длина основания
S = π*R*L ; S = 3,14 * 2 * 4,03 = 6,28 * 4,0311 = 25,31 м^2
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y1(x) и y2(x) - непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций yi(x) по переменной x
Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) - однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле
Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. "Практикум из математического анализа" (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.
Пошаговое объяснение: