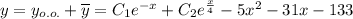27=3³ значит сложили 3 кубика в длину, 3 в ширину, 3 в высоту.
Каждая грань куба состоит из 3*3=9 кубиков.
1) 9*6=54 граней маленьких кубиков раскрашено
2) Только 1 кубик находится внутри куба, поэтому нераскрашенным окажется только 1 кубик.
3) Кубики, у которых раскрашена только одна грань, это кубики в центре каждой грани большого куба - таких 6.
4) На каждом ребре большого куба находится по 3 маленьких кубика. Верхние и нижние имеют по 3 ребра соприкосновения, а средний 2.
Значит в каждом ребре по 1 кубику - 12 кубиков
5) Это те кубики которые находятся в вершине куба - таких кубиков 8.
6) Нет, таких кубиков нет. Т.к. каждый кубик, хотя бы одной гранью обращен внутрь.
Найдем сначала общее решение соответствующего однородного дифференциального уравнения
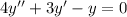
Пусть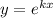 
, мы получим характеристическое уравнение
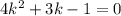
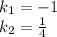
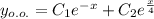— общее решение однородного диф. ур.
Найдём теперь частное решение. Рассмотрим функцию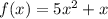 
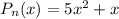отсюда 
; 
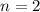. Сравнивая 
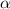с корнями характеристического уравнения и, принимая во внимая, что , частное решение будем искать в виде:
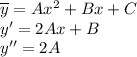
Подставляем в исходное дифференциальное уравнение
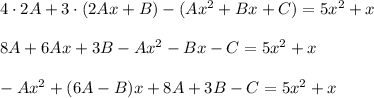
Приравниваем коэффициенты при степени x
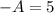откуда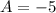 
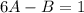откуда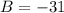 
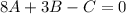откуда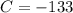 
Частное решение: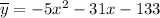 
Общее решение линейного неоднородного дифференциального уравнения:
