128
Пошаговое объяснение:
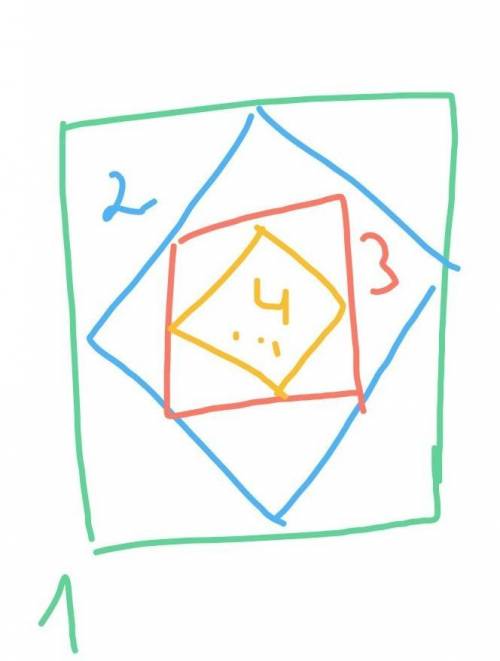
Пусть сторона квадрата 1 равна а, тогда половина его стороны равна а/2, а длина отрезка соединяющего середины его сторон (длина стороны квадрата 2) равна:√( (а/2)² + (а/2)²) = √ (2а²/4) = а / √2.
Половина стороны квадрата 2 равна а /2√2.Тогда длина отрезка соединяющего середины его сторон (длина стороны квадрата 3) равна:√ ( (а/2√2)² + (а/2√2)² ) = √ (2а²/8) = а / 2.
И так далее ...Тогда площадь первого квадрата:
S1 = a*a = а²
Площадь второго квадрата:
S2 = (a / √2)² = а²/2.
Площадь третьего квадрата:
S3 = (a/2)² = a² / 4.
И так далее...
Заметим, что площадь каждого следующего квадрата меньше предыдущего в 2 раза.
То есть получаем геометрическую прогрессию со знаменателем q = 1/2.
Следовательно, сумма бесконечно убывающей геометрической прогрессии:
S∞ = b1 / (1-q).
в данном случае:
q=1/2, 1-q=1-1/2=1/2;b1=S1=a²;a = 8, b1=8² = 64.S∞ = 64/(1/2)=64*2=128
х второе число
2х первое число
2х+2,3 третье число
составим уравнение:
(х+2х+2х+2,3):3=7,4
х+2х+2х+2,3=7,4*3=22,2
5х=22,2-2,3=19,9
х=3,98 второе число
3,98*2=7,96 первое число
7,96+2,3=10,26 третье число
проверка:
(3,98+7,96+10,26):3=7,4
22,2/3=7,4
7,4=7,4
Пошаговое объяснение: