Пошаговое объяснение:
80% качественных тарелок из 120 завезённых тарелок:
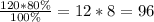 (тарелок). ⇒
(тарелок). ⇒
С деффектами завезли: 120-96=24 (тарелки).
Количество дефектных тарелок, которые еще можно
использовать в работе равно:
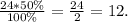 ⇒
⇒
На раздаче в зале было: 96+12=108 (тарелок).
Вероятность, что первая взятая в зале на раздаче тарелка
окажется без дефекта равна:
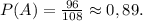
ответ: P(A)≈0,89.
Пусть х км/ч скорость второго авто, тогда (х+20) км/ч скорость первого. Замечаем, что 2 ч 24 мин = 2,4 ч , составляем уравнение по времени в пути двух авто:
420 / х - 420 / (х+20) = 2,4
Приводим к общему знаменателю х(х+20) и
отбрасываем его, записав, что х не=0 и х не=-20
420(х+20)-420х=2,4х(х+20)
420х+8400-420х = 2,4x^2+48х
2,4x^2+48x- 8400 =0
x^2+20x-3500=0
D= 400+4*3500=14400, 2 корня
х(1)=(-20+120)/2 = 50 (км/ч ) скорость второго авто
х(2)= (-20-120)/2= -70 не подходит под усл задачи
50+20=70 км/ч скорость первого авто
6
5
(7+9y)≤14
3
2
−
8
7
(5y−8)
6
5
(7+9y)≤
3
44
−
8
7
(5y−8)
6
5
∗7+
6
5
∗9y≤
3
44
−
8
7
∗5y−
8
7
∗(−8)
6
35
+
6
45y
≤
3
44
−
8
35y
+
8
56
6
45y
+
8
35y
≤
3
44
+
8
56
−
6
35
24
180y
+
24
105y
≤
24
352
+
24
168
−
24
140
\begin{gathered}\frac{285y}{24}\leq\frac{520}{24}-\frac{140}{2}frac{285}{24}y\leq\frac{380}{24}y\leq \frac{380}{24}:\frac{285}{24}y\leq \frac{380}{24}*\frac{24}{285}y\leq \frac{76}{1} *\frac{1}{57}y\leq \frac{76}{57}y\leq1 \frac{19}{57}y\leq 1\frac{1}{3}\end{gathered}
24
285y
≤
24
520
−
2
140
24
285
y≤
24
380
y≤
24
380
:
24
285
y≤
24
380
∗
285
24
y≤
1
76
∗
57
1
y≤
57
76
y≤1
57
19
y≤1
3
1
y ∈ ( -∞ ; 1\frac{1}{3}1
3
1
]
0,11
Пошаговое объяснение:
в зал на раздачу могут попасть только тарелки, которые можно использовать
120 * 0,2 = 24 (тарелки) - с дефектами
24 * 0,5 = 12 (тарелок) - с дефектами можно использовать
A - выбранная тарелка с дефектом
P(A) = m/n
m - количество благоприятных исходов
n - количество всех исходов
m = 12
n = 120 - 12 = 108
P(A) = 12/108 = 1/9 ≈ 0,11