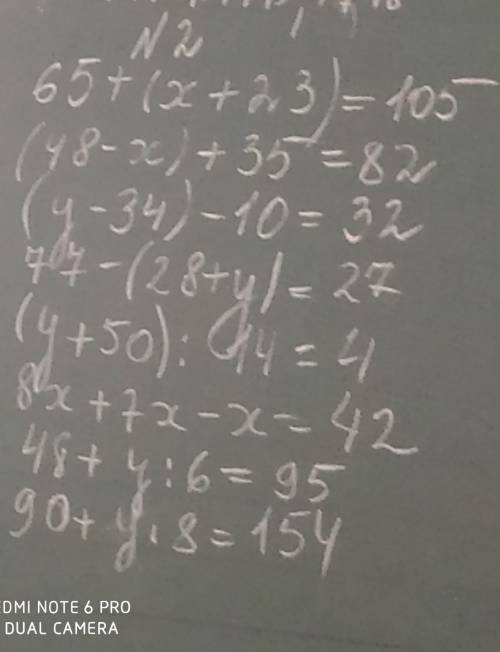
65+(х+23)=105
65+х+23=105
х+88=105
х=105-88
х=17
ответ: 17.
(48-х)+35=82
48-х+35=82
83-х=82
х=83-82
х=1
ответ:1.
(у-34)-10=32
у-34-10=32
у-44=32
у=44+32
у=76
ответ: 76.
77-(28+у)=27
77-27-у=27
50-у=27
у=50-27
у=23
ответ: 23.
(у+50):14=4
у+50=14×4
у+50=56
у=56-50
у=6
ответ: 6.
8х+7х-х=42
14х=42
х=42:14
х=3
ответ: 3.
48+у:6=95
у:6=95-48
у:6=47
у=6×47
у=282
ответ: 282.
90+у:8=154
у:8=154-90
у:8=64
у=8×64
у=512
ответ: 512.
Первый путь решения:
это уравнение в полных дифференциалах.
Потому что
dP/dy=dQ/dx.
где
Р=(2x-y+1)
Q=(2y-x-1)
Надо найти такую функцию U(x;y), что
dU/dx=P
dU/dy=Q.
Тогда решение будет U=C.
С одной стороны
dU/dx=2x-y+1
U= x^2-xy+x +C1(y)
С другой стороны
dU/dy=2y-x-1
U=y^2-xy-y+C2(x)
x^2-xy+x +C1(y)=y^2-xy-y+C2(x)
x^2+x +C1(y)=y^2-y+C2(x)
C1(y)=y^2-y
U= x^2-xy+x +C1(y)= x^2-xy+x +y^2-y=C
Второй путь решения.
Это уравнение, сводящееся к однородному.
(2x-y+1)dx+(2y-x-1)dy=0
сгруппируем так:
(2(x+1/3) - (y-1/3))dx+(2(y-1/3)- (x+1/3))dy=0
замена
a=x+1/3; da=dx
b=y-1/3; db=dy
(2a-b)da+ (2b-a)db=0- однородное
вводим новую функцию
b/a=u
b=ua
db=uda+adu
(2a- ua)da+ (2ua-a)(uda+adu)=0
(2- u)da+ (2u- 1)(uda+adu)=0
(2+ 2u^2- 2u)da+ (2u-1)adu=0
разделяем переменные
∫da/a= 1/2*∫(1-2u)du/( u^2- u+1)
заметим, что (1-2u)du= -d(u^2- u+1)
ln(C*|a|)=-1/2 *ln(C|(u^2- u+1|)
откуда
a=C/√(u^2- u+1)
a*√((b/a)^2- b/a+1)=C
√((b^2- b*a+a^2)=C
(y-1/3)^2- (y-1/3)(x+1/3)+(x+1/3)^2=C^2
Пошаговое объяснение:
1) х+23=105-65
х+23=40
х=40-23
х=17
2)48-х=82-35
48-х=47
х=48-47
х=1
3)у-34=32+10
у-34=42
у=42+34
у=76