Объем конуса = 96π куб. единиц.
Пошаговое объяснение:
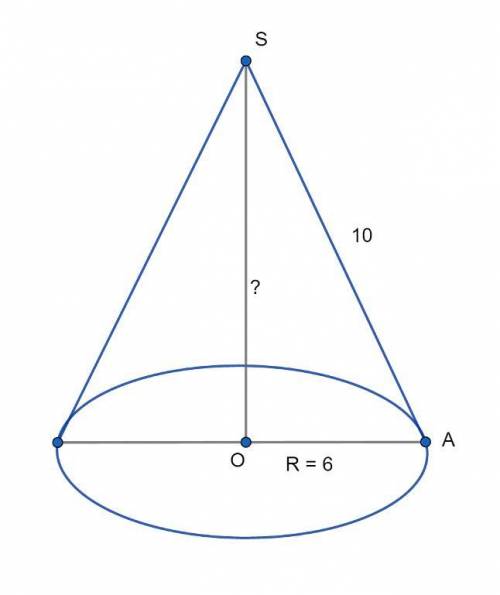
Рисунок в приложении.
Объем конуса равен произведению одной трети площади основания на высоту. Vкон =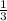 
* Sосн * H = 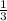* πR² * H;
Так как по условию диаметр основания конуса D = 12, то его радиус R = D/2 = 12/2 = 6.
ΔSOA прямоугольный, ∠SOA = 90°, SO - высота конуса, образующая конуса SA = 10, радиус основания OA = 6. По т. Пифагора найдем высоту конуса:
SO² = SA² - OA² = 10² - 6² = 100 - 36 = 64;
Высота конуса H = SO =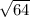 
= 8.
Найдем объем конуса:
Vкон = 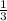* π * 6² * 8 = 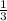* π * 36 * 8 = π * 12 * 8 = 96π (куб. единиц).
Vкон = 96π куб. единиц.
1.
а) –2 < 5; б) –6 > –7; в) 2,5 > - 2,5; г) 3 > –1,5;
д) 36,5 > 0; е) –8,2 < 0; ж) 6,2 > 6,12; з) 0, 149 < 0,6
2.
а) 1,4 + 4,12=5,52
б) (–7) + (+3,6)= -3,4
в) –7 + 23=16
г) 2,6 + (–1,1)=1,5
д) (–4,9) + (–1,1)= -6
е) –3 + 3=0
3.
а) 6,37– (–14,1)=20,47
б) 2,66 –1,14=1,52
в) –7,44 – (–43,6)=36,16
г) – 4,09 –1,71= - 5,8
д) –7– 2= -9
е) –3 – 7= -10
4.
1) -(-3)· 5 = 15
2) -6:1= -6
3) -0,5∙(-0,9) = 0,45
4) -2,8 : 7= -0,4
5.
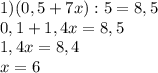
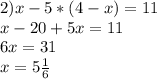
6.
8<9<12
8<10<12
8<11<12
ответ 9,10,11
Пошаговое объяснение:
Достаточно?