Отметь как лучшее
А1. Расположи числа в порядке убывания:
2) 13 803, 10 853, 10 385, 1335, 8003
А2. Замени число 690 171 суммой разрядных слагаемых.
1) 600 000 + 90 000 +100+70 + 1
A3. Найди число, которое состоит из 1 единицы пятого раз¬ряда, 2 единиц четвертого разряда, 3 единиц третьего разряда и 6 единиц первого разряда.
3)12306
А4. При делении на круглые числа 10, 100, 1000:
3) в частном всегда получаем ноль
А5. Найди ошибки.
1)738 + 0=738-0
3)617-1=616
А6. Какое число соответствует высказыванию: 2 млн 8 тыс. 3 сот. 4 дес. 6 ед.
2)2 008346
А7. В каком числе всего 54 тысячи?
4) 54 456
Пошаговое объяснение:
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
C =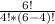 
= 15 возможностей их различной посадки
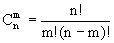
- Х = - 0,8
Х = +0,8 (понимаешь? знак переносится из левой части вправо и знак меняется с минуса на плюс!)
- Х = - 4 1/3;
- Х = 5/6 - 1/9
Х = - (5/6 - 1/9) приводим к общему знаменателю
Х = - (45/54 - 6/54) = -39/54
Х = -13/18;
- Х = - 7,2
Х = - (- 7,2) = 7,2;
- Х = 3/8+1/6
Х = - (3/8+1/6)
Х = - (18/48+8/48)
Х = - (26/48)
Х = - 13/24
Пишу специально так подробно, чтобы тебе было понятно! Чтобы разобраться раз и навсегда! ))) Удачи!