Пошаговое объяснение:
продифференцируем F(x)
F'(x) = 2/3 * 3x² - 4 * 2x + 6 = 2x² - 8x + 6 = f(x) => F(x) первообразная для f(x)
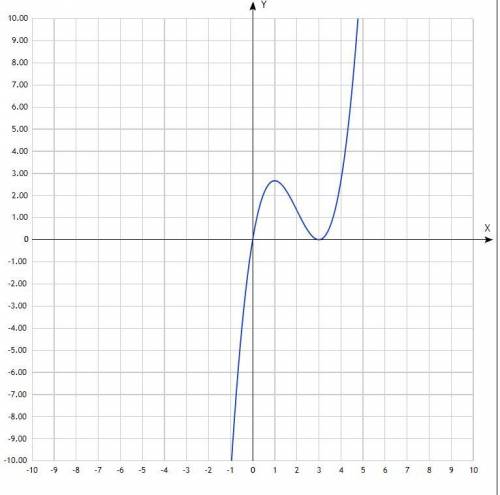
б) решим уравнение f(x) = 0
x² - 4x + 3 = 0
(x - 3)(x - 1) = 0
x₁ = 1; x₂ = 3 - экстремумы
F(-1) = -2/3 - 4 - 6 = -10 2/3 - наименьшее значение
F(1) = 2/3 - 4 + 6 = 2 2/3
F(3) = 18 - 36 + 18 = 0
F(4) = 128/3 - 64 + 24 = 2 2/3
г) F(x) = bx
2x³ - 12x² + 18x = 3bx
x(2x² - 12x + 18 - 3b) = 0
x₁ = 0 -первый корень
значит квадратный трехчлен должен иметь ровно один корень
для этого D = 0
D = 144 - 8(18 - 3b) = 0
18 - 3b = 144/8
18 - 3b = 18
3b = 0
b = 0
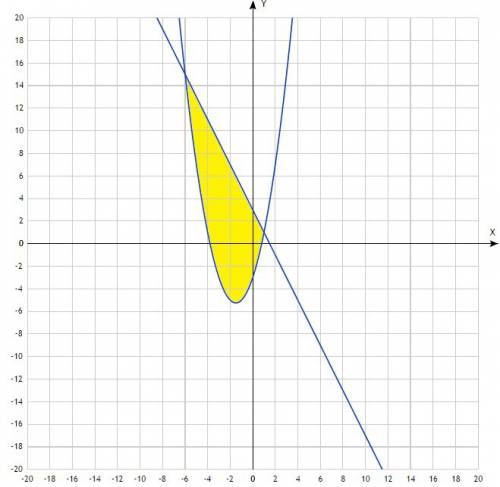
в) в приложении
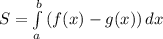



 ед².
ед².