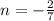Весь путь туристы с одинаковой скоростью за два дня. в первый день они были в пути 9 ч, во второй 6 ч. во второй день они на 15 км меньше, чем в первый. сколько км туристы за два дня

👇

Ответ:

diaweeti551

24.04.2021

1)9-6=3(ч) на столько часов шли меньше.
2,15/3=5(км/ч) скорость туристов за 3 часа.
3)9+6=15(ч) всего шли туристы.
4)5*15=75(км туристы за 2 дня.
ответ:75км.

4,8(69 оценок)

Открыть все ответы

Ответ:

LoveSmile78900987

24.04.2021

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

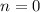- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

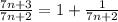
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

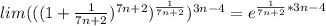$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

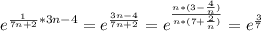$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

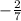
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

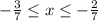Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

4,4(95 оценок)

Ответ:

Arcator

24.04.2021

а)

Построение

1. Допустим, что MN не параллельна АВ.

2. Продолжим MN и АВ до пересечения их в т. О.

3. ОК ⊂ пл. АВС (т.к. О ∈ АВС и K ∈ АВС).

4. Соединим точки K и N.

5. Плоскости ONK и ОАK (то есть пл. АВС) пересекаются по прямой OK.

6. Поэтому продолжим OK до пересечения с DC в т. L. Соединим точки K и L - ведь они лежат в одной плоскости.

7. Противоположные грани АА1В1В и DD1C1C секущая плоскость пересечет по параллельным прямым (по теореме II), поэтому в плоскости DD1C1C проведем LP || NM.

8. Соединим т. Р и т. М.

9. MNKLP - искомое сечение.

ВОТ НАДЕЮСЬ