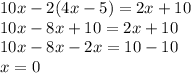№ 2:
при каком значении параметра a уравнение |x^2−2x−3|=a имеет три корня?
введем функцию
y=|x^2−2x−3|
рассмотрим функцию без модуля
y=x^2−2x−3
y=(x−3)(х+1)
при х=3 и х=-1 - у=0
х вершины = 2/2=1
у вершины = 1-2-3=-4
после применения модуля график отражается в верхнюю полуплоскость
при а=0 - 2 корня (нули х=3 и х=-1)
при 0< а< 4 - 4 корня (2 от исходной параболы, 2 от отображенной части)
при а=4 - 3 корня (2 от исходной параболы, 1 от вершины х=1)
при а> 4 - 2 корня (от исходной параболы)
ответ: 4
1. Немного непонятно выражение.
2. Так как количество груш, растущих в саду, составляет 32% количества яблонь, находим:
50*0,32 = 50*32/100 = 16 груш
Найдем, какое количество вишен растет в саду (обозначим через х), если груши составляют 4/7 от количества вишен:
х*4/7 = 16
х = 16*7/4 = 28
ответ: 16 груш, 28 вишен.
3. На фото ниже.
4. Пусть первый вагон - 3х, тогда второй - х. Когда из первого вагона вышло 28 пассажиров - (3х-28), а из второго 4 пассажира (х-4), то в обоих вагонах пассажиров стало поровну. Составим уравнение:
3х - 28 = х - 4
2х = 24
х = 12 (п.) - во 2 вагоне
12*3 = 36 (п.) - в 1 вагоне
ответ: 36 пассажиров, 12 пассажиров.
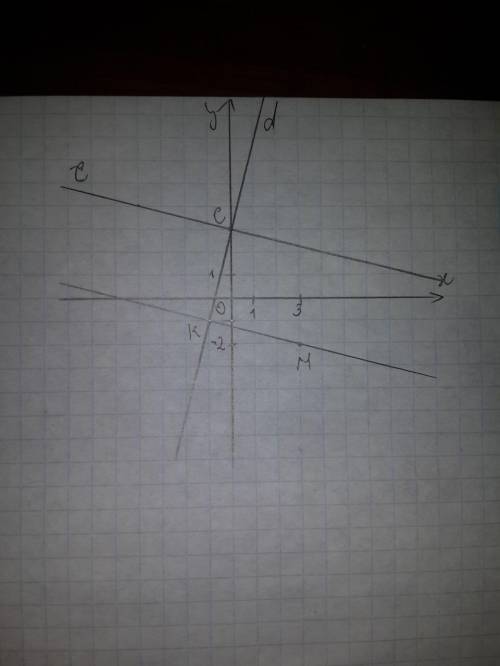
5.