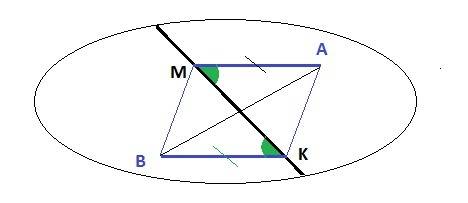
Дано: MA=KB, ∠AMK=∠BKM
∠AMK=∠BKM - накрест лежащие углы равны при секущей MK, следовательно, прямые MA║KB
MA = KB, MA║KB ⇒ BMAK - параллелограмм. MK и AB - его диагонали.
Какое утверждение верно ?
1. ΔAMB=ΔAKB ВЕРНО
Диагональ AB параллелограмма разбивает его на два равных треугольника.
2. ∠AKM = ∠BMK ВЕРНО
Это накрест лежащие углы при BM║AK и секущей MK
3. ΔMKA = ΔKMB ВЕРНО
Диагональ MK параллелограмма разбивает его на два равных треугольника. Эти треугольники равны по двум равным сторонам и углу между ними.
4. ∠AMB = ∠KBM НЕВЕРНО
Соседние углы параллелограмма будут равны только в том случае, если параллелограмм является прямоугольником. Для произвольного параллелограмма соседние углы в сумме дают 180°, но не равны.
утята - 6 лап
медвежата - 8 лап
зайцы - 20 лап
итого: 38 лап ( 4+6+8+20)