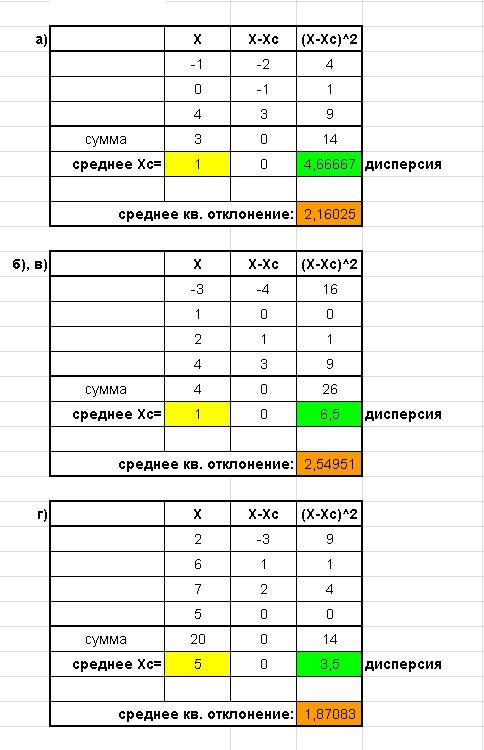
Картинка с табличками вложена. Искомые величины выделены цветом.
а)
Сначала находим среднее значение выборки:
Хс = (-1 + 0 + 4)/3 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n}} = \\
\sqrt{\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 2,1602
Дисперсия - это средний квадрате отклонений от средней величины:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n} = \\
\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 4,6667
б)
Среднее значение выборки:
Хс = (-3 + 1 + 2 + 4)/4 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 2,5495
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} = \\
\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 6,5
в) смотри б)
г)
Среднее значение выборки:
Хс = (2 + 6 + 7 + 5)/4 = 5
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 1,8708
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} =
\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 3,5
Вместе ребята собрали всего 18 кристаллов
Пошаговое объяснение:
одна часть - х, тогда собрали:
Коля - 2х (кристаллов);
Вася - 4х (кристаллов);
Павел - 3х (кристаллов)
По условию 4х-2х=4, т.к. Вася собрал на 4 кристалла больше чем Коля
1) Найдем х:
4х-2х=4
2х=4
х=4:2
х=2 (кристалла) - составляет одна часть
2)Найдем сколько кристаллов собрал каждый:
2х=2*2=4 (кристалла) - собрал Коля;
4х=4*2=8 (кристаллов) - собрал Вася
3х=3*2=6 (кристаллов) - собрал Павел
3)Найдем сколько собрали всего ребята:
4+8+6=18 (кристаллов)
Последние действия (№2 и №3) можно заменить одним
2х+4х+3х=9х=9*2=18 (кристаллов) - всего собрали
(0,00625*1.8)*(8*2)=0,01125*16=0.18