В решении.
Пошаговое объяснение:
Рациональные числа в быту.
Сначала нужно определить, какие числа являются рациональными.
Рациональные числа, включают целые, дробные числа и нуль.
Целые числа включают целые положительные, целые отрицательные и нуль.
Натуральные числа включают целые положительные.
Дробные включают обыкновенные, конечные и периодические.
В быту люди используют все указанные рациональные числа, только целые отрицательные как числа используются редко.
Когда мы считаем что-то, используем натуральные числа: 5 яблок, три апельсина, 10 конфет.
Когда сообщаем кому-то, который час, 3 часа дня или 7 часов вечера, используем также натуральные числа.
Когда делим что-то на части: режем торт, яблоко, используем дробные числа: говорим четвертинка яблока (1/4), половина торта (1/2), полстакана чая (1/2).
Ноль как число используем, когда говорим: ничего нет, пусто.
Сторона квадрата: 12 м
Радиус полукруга: 6 м
Длинна забора: 72 м
Пошаговое объяснение:
Площадь всей фигуры это сумма площадей квадрата и 4 полукругов. Но так же по рисунку видно что 4 полукруга можно представить как два одинаковых круга с диаметром а, который так же равен стороне квадрата. Распишем площади отдельно:
Квадрата:
S = a × a = a²
Кругов:
S = п × R² = п × 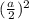
Общая площадь всей фигуры тогда:
S = a² + п × 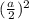 + п ×
+ п × 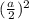
Подставим значения которые у нас есть и решим уравнение:
360 = a² + 3 × 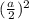 + 3 ×
+ 3 × 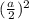
360 = а² + 2 × 3 × 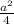
360 = a² + 3 × 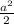
360 = 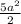
72 = 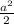
144 = a²
a = 12 м
Тогда:
R = а ÷ 2 = 12 ÷ 2 = 6 м
Длина забора тогда равна сумме 4 дуг полукругов:
L = 4 × п × R / 180 × 180 = 4 × 3 × 6 = 72 м
1) х+у=1780
2) х÷у=1ч (52) это есть х+52=у
3) х=1780-у
1780+52-у=у
2у=1832
У=916
х=864
864+916=1780