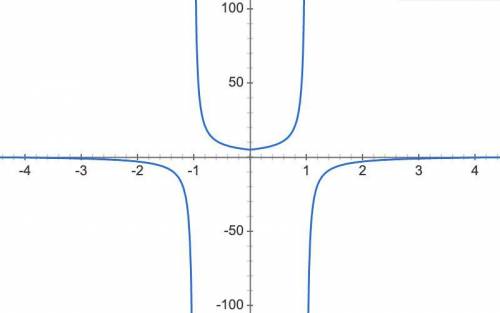
В функции переменная x всегда используется по модулю, поэтому график функции будет симметричен относительно оси ординат (OY), а для построения всего графика достаточно построить правую часть (при x ≥ 0), после чего отразить влево.
При x ≥ 0 исходная функция приобретает вид:
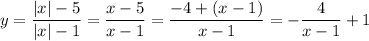
Для построения графика этой функции можно последовательно:
Построить график функции y = 1 / xСдвинуть график вправо на 1Вытянуть график вдоль вертикальной оси OY в 4 разаОтразить график относительно горизонтальной оси OXСдвинуть график вверх на 1Теперь осталось правую часть получившегося графика (при x ≥ 0) зеркально отразить влево относительно вертикальной оси OY.
Чтобы выяснить область значений функции, можно рассмотреть отдельно ветви гиперболы на графике при x ≥ 0. С правой ветвью всё просто: она дает область значений от (–∞; 1), т.к. гипербола сдвинута вверх на 1. А левая ветвь давала бы область значений (1; +∞), но она ограничена слева осью OY и в этой точке f(0) = 5, поэтому левая ветвь дает область значений [5; +∞). Область значений всей функции -- объединение областей левой и правой ветви: (–∞; 1) ∪ [5; +∞).
Область определения функции обусловлена тем, что знаменатель дроби не должен быть равен нулю, т.е. |x| – 1 ≠ 0, что выполняется при x ≠ -1, x ≠ 1.
Область значений фунцкии: y ∈ (–∞; 1) ∪ [5; +∞).
Область определения функции: x ∈ (–∞; +∞) \ {-1; 1} (или x ≠ -1, x ≠ 1).
Промежутки монотонности: убывает на интервале x∈(-∞; 0), возрастает на интервале (0; +∞).
1) 2 сад имеет большую площадь на 227,205 м²
2) на ограждение 1 сада уйдет меньше матерьяла
Пошаговое объяснение:
а₁=b₁*0,75
а₁=50,4*0,75
а₁=37,8 м
b₂=a₂*1,3
b₂=40,5*1,3
b₂=52,65 м
S₁=a₁*b₁
S₁=37,8 *50,4
S₁=1905,12 м² площадь первого сада
S₂=a₂*b₂
S₂=40,5*52,65
S₂=2132,325 м² площадь 2 сада
2132,325-1905,12=227,205 м² площадь второго сада больше площади первого
P₁=2(a₁+b₁)
P₁=2(37,8+50,4)
P₁=176,4 м длина первого ограждения
P₂=2(a₂+b₂)
P₂=2(40,5+52,65)
P₂=186,3 м длина второго ограждения
176,4 < 186,3 P₁< P₂ на ограждение 1 сада уйдет меньше матерьяла