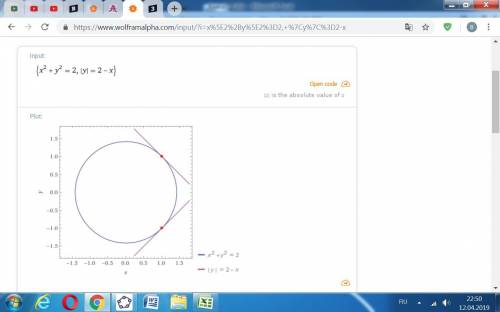
Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
Пошаговое объяснение:Для того, чтоб найти длину отрезка KN необходимо знать с каких отрезков состоит этот отрезок. Известно, что точки M,K и N лежат на одной прямой. Если необходимо найти длину отрезка KN, то это значит, что точки K и N, расположены по краям отрезка, а точка М делит этот отрезок на две части. Для того, чтоб найти длину отрезка KN, необходимо сложить отрезки МK и МN, длины этих отрезков известны :
KN = МK + МN ;
Запишем в численных значениях :
15 + 6 = 21 (см) - длина отрезка KN
ответ : 21 см