3
Пошаговое объяснение:
Всего было n * (n - 1) / 2 игр между профессионалами (в каждой такой игре победил профессионал), 2n * (2n - 1)/2 игр между любителями (соответственно, в таких играх побеждали любители) и n * 2n = 2n^2 игр, в которых приняли участие профессионал и любитель (допустим, в x из них победил профессионал, и в 2n^2 - x победил любитель).
Оценим возможное отношение числа побед профессионалов к числу побед любителей, оно равно
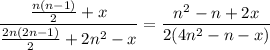 [*}
[*}
Это отношение будет наименьшим при x = 0, когда все любители обыграли всех профессионалов, тогда оно равно (n - 1)/(8n - 2).
Это отношение будет наибольшим при x = 2n^2 (это соответствует всем поражениям любителей в матчах с профессионалами), значение отношения (5n - 1)/(4n - 2).
Найдем, при каких n 7/5 попадает в этот промежуток:
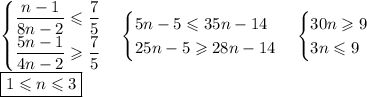
Итак, все возможные n - 1, 2 и 3. Заметим, что общее количество игр 3n (3n - 1)/2 должно быть кратно 7 + 5 = 12, это выполнено только для n = 3.
53 + 18 = ( 50 + 3) + ( 10 + 8) = ( 50 + 10) + ( 3 + 8) = 60 + 11 = 71
53 + 28 = ( 50 + 3) + ( 20 + 8) = ( 50 + 20) + ( 3 + 8) = 70 + 11 = 81
53 + 38 = ( 50 + 3) + ( 30 + 8) = ( 50 + 30) + ( 3 + 8) = 80 + 11 = 91
вычислив первый пример, можем заметить, что в каждом следующем, второе слагаемое на десяток больше, не вычисляя можно написать ответы))
73 + 17 = ( 70 + 3) + ( 10 + 7) = (70 + 10) + ( 3 + 7) = 80 + 10 = 90
73 + 19 = ( 70 + 3) + ( 10 + 9) = ( 70 + 10) + ( 3 + 9) = 80 + 12 = 92
73 + 18 = ( 70 + 3) + ( 10 + 8) = ( 70 + 10) + ( 3 + 8) = 80 + 11 = 91
55 + 29 = ( 50 + 5) + ( 20 + 9) = ( 50 + 20) + ( 5 + 9) = 70 + 14 = 84
46 + 38 = ( 40 + 6) + ( 30 + 8) = ( 40 + 30) + (6 + 8) = 70 + 14 = 84
37 + 47 = ( 30 + 7) + ( 40 + 7) = ( 30 + 40) + ( 7 + 7) = 70 + 14 = 84
7.5*100%:20%=37.5м
0.75*100%:20%=3.75м
22.22*100%:20%=111.1м
100*100%:205=500м
236*100%:20%=1180м