Пошаговое объяснение: а) f(x)= x³ -3x ⇒ f'(x)=3x² - 3. Найдём критические точки: f'(x)=0 ⇒ 3x² - 3=0 ⇒ x²-1=0 ⇒x²=1 ⇒ x₁₂=±1/ Но х= -1 ∉ [0;3], значит х=1 -крит.точка. Найдём значения функции в критической точке и на концах промежутка: f(1)=1³ - 3·1 = -2 f(0)=0³- 3·0= 0 f(3)= 3³-3·3=18. Cледовательно max f(x)=f(3)=18, min f(x)=f(1)= - 2 б) f(x)= x⁴-2x²+3 ⇒ f'(x)= 4x³-4x . Если f'(x)=0, то 4x³-4x =0 ⇒ x(x-1)=0 ⇒ x₁=0, x₂=1 -критические т.очки, они ∈[0 ; 2]. Найдём значения функции в критических точкач и на концах промежутка: f(0) =3
f(1)=1⁴-2·1²+3=2 f(2)=16-8+3=11. Cледовательно max f(x)=f(2)=18, min f(x)=f(1)= 2
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
пути.
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
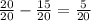
50 км =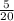 
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км = 
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
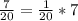
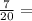10 км * 7 = 70 км.
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
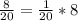
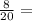10 км * 8 = 80 км.
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.
2) 16 * 5N = 80N (ОТВЕТ)