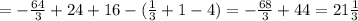 ед²
ед²
Разложим 105 на простые множители: 105=3*5*7. Значит натуральное число состоит из цифр 3,5 и 7. Это могут быть числа 357, 375, 537, 573, 735 и 753. Разложим 99 на простые множители: 99=3*3*11. Следовательно делителями могут быть числа 3, 9, 11, 33 и 99. Число делится на 3 если сумма его цифр делится на 3. 3+5+7=15; значит наше натуральное число делится на 3. Признак делимости на 9 тот же. Поскольку 15 на 9 не делится, то и наше натуральное число не делится на 9. Если знакопеременная сумма цифр числа делится на 11, то и само число делится на 11. Поскольку 3-5+7=5, 3-7+5=1 и 7-3+5=9 не делятся на 11, то и наше число на 11 не делится. Следовательно не делится оно и на 33 и на 99. Значит НОД натурального числа и 99 равен 3.
ответ: 3.
1) - 7 + х = 13 2) х + (- 9) = - 4
х = 13 + 7 х = - 4 + 9
х = 20 х = 5
- 7 + 20 = 13 5 + (- 9) = - 4
13 = 13 - 4 = - 4
3) х + (- 15) = 10 4) 8 + х = - 12
х = 10 + 15 х = - 12 - 8
х = 25 х = - 20
25 + (- 15) = 10 8 + (- 20) = - 12
25 - 15 = 10 8 - 20 = - 12
10 = 10 - 12 = - 12
5) - 6 + х = 5 6) х + (- 14) = - 8
х = 5 + 6 х = - 8 + 14
х = 11 х = 6
- 6 + 11 = 5 6 + (- 14) = - 8
5 = 5 6 - 14 = - 8
- 8 = - 8