1)
Для того, чтобы число делилось на 15,оно должно делиться на 3 и на 5.
2)
Для того, чтобы число делилось на 3, сумма его цифр должна делиться на 3.
3)
Для того, чтобы число делилось на 5, последняя цифра должна быть равна 5 либо 0.
4)Из третьего пункта нам не подходит последняя цифра 0, так как все, что умножается на ноль равно нулю.
Примем наше число за набор переменных:
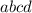
Из пункта 4) следует:
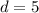
Из условия следует:

Так как мы знаем, что d=5,то
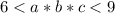
Теперь начнём подбор:
1)
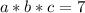
Тогда одно число будет равно 7, а два других - единице.
Проверим выполняемость пункта 3):
7+1+1+5=14
14 не делиться на три без остатка.
Значит, это нам не подходит.
2)
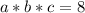
а) Одно число равно 8,а остальные два других - единице.
Проверим выполняемость пункта 3):
8+1+1+5=15
Число 15 делиться целочисленно на 3.
Одно число найдено:
8115б) Одно число равно четверке, другое двойке, а третье единице.
П. 3):
4+2+1+5=12
Верно.
Ещё одно число:
4215в) Каждое из этих трёх чисел равно двойке.
П. 3):
2+2+2+5=11
Проверка не пройдена.
Из найденных чисел наибольшим является число 8115.Проверка условий задачи:
Произведение цифр:
8*1*1*5=40
Пройдено.Кратность 15:
8115/15=541
Пройдено.Четырехзначное?
Да. ответ: 8115.Первый ряд:
Делаем вывод из наших примеров и получаем что к первому числу нужно прибавить 2, ко второму 4, и так далее.
Закономерность меняется на +2 каждый раз.
22-14=8
14-8=6
8-4=4
4-2=2
ответ: 2,4,8,14,22,32,44,58.
Второй ряд:
Делаем вывод из вычислений, каждое число нужно умножить на три (*3)
27/9=3
9/3=3
3/1=3
ответ: 1,3,9,27,81,243,729.
Третий ряд:
Также из примеров делаем вывод и получаем что нужно вычесть двенадцать и к следующему числу прибавить семь (-12,+7)
89-77=12
89-82=7
94-82=12
94-87=7
99-87=12
ответ: 99,87,94,82,89,77,84,72,79.