Я могу дать только одну интерпретацию условия: доказать, что число 2528 нельзя представить в виде суммы
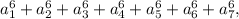
где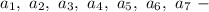 
целые числа. Такую задачу я и буду решать.
Поскольку шесть четное число, достаточно доказать утверждение для неотрицательных целых чисел. Имеем:
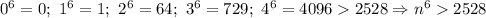
при n>3. Поэтому надо пытаться делать 2528 из чисел 0, 1, 64 и 729.
Если использовать только первые три числа, то сумма будет не больше чем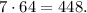 
До 2528 мы не дотянули на 2528-448=2080 единиц. Значит, надо использовать и 729, причем поскольку
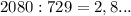, 729 нужно использовать как минимум 3 раза, а поскольку 729·4=2916>2528, число 729 нужно использовать ровно 3 раза. Теперь задача сводится к более простой:
2528-729·3=2528-2187=341; число 341 нужно представить в виде суммы четырех чисел, используя только 0, 1, и 64. Однако такая сумма заведомо не может быть больше, чем 4·64=256.
Следовательно, мы доказали, что число 2528 нельзя представить в виде суммы семи шестых степеней целых чисел.
aaa×a=5439
Все эти переменные - одинаковые числа, значит нужно найти на какие числа делится:
Нам нужно ТРЕХЗНАЧНОЕ число, которое при умножении на ОДНОЗНАЧНОЕ число даст 5439.
5439 делить на 1 - нет смысла,
5439 делить на 2 - нет смысла, получится не целое число,
5439 делить на 3 - 1813, но это четырехзначное число, а так же разряды не одинаковые,
5439 не делится на 4, получится не целое число,
5439 не делится на 5, признак делимости на 5 - если числа заканчиваются на 0 и 5.
5439 не делится на 6, так как в таблице умножения 6 нет чисел, которые оканчиваются на 9.
5439 ДЕЛИТСЯ на 7, и ответом будет 777, мы нашли правильный ответ:
777*7=5439