Пошаговое объяснение:
ОДЗ: выполняется при всех значениях х, т.к. sinx и sin2x ∈ [-1;1], даже в худшем случае b = -1 - 1 + 16 = 14 > 0
Чтобы весь этот логарифм равнялся 2, нужно,чтобы
синусы были равны 0
log4 (16) = 2
sinx + sin2x = 0
sinx + 2sinx * cosx = sinx * (1 + 2cosx) = 0
sinx = 0
x1 = pin, n ∈ Z
1 + 2cosx = 0
cosx = -1/2
x2 = 2pi/3 + 2pik
x3 = 4pi/3 + 2pik, k ∈ Z
б) -4pi ≤ pin ≤ -5pi/2 | :n
-4 ≤ n ≤ -2,5
n = -4
n = -3
x1 = -4pi
x2 = 3pi
-4pi ≤ 2pi/3 + 2pik ≤ -5pi/2
-4pi - 2pi/3 ≤ 2pik ≤ -5pi/2 - 2pi/3
- 14pi/3 ≤ 2pik ≤ -19/6 | :2pi
-7/3 ≤ k ≤ -19/12
k = -2
x3 = 2pi/3 + 2pi*(-2) = -10pi/3
-4pi ≤ 4pi/3 + 2pik ≤ -5pi/2
-4pi - 4pi/3 ≤ 2pik ≤ -5pi/2 - 4pi/3
- 16pi/3 ≤ 2pik ≤ -23pi/6 | :2pi
-8/3 ≤ k ≤ -23/12
k = -2
x3 = 4pi/3 + 2pi*(-2) = -8pi/3
Пошаговое объяснение:
если взять 5 яблок и поделить из всек на 10терых человек, нужно будет каждое яблоко разрезать на 2 части и каждая половинка будет результатом деления 5 на 10. Дробь это как бы часть числа 1 (в нашем случае яблока), а поскольку того, что надо поделить меньше, чем количества частей на которое его делят, то целых чисел не хватает и приходится использовать дроби(части числа). У любого числа x обратное ему равно
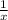
то есть у числа 13:
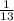
у числа 69:
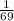
и так далее.
Их не обязательно использовать при деление, это видимо придумали тупорылые авторы учебников, а чтобы поделить дробь на число, достаточно нижнюю часть дроби (так называемый знаминатель) умножить на то самое число, таким образом:
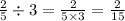
Пошаговое объяснение:
2y'' - y' - y = e^x + sin x
Характеристическое уравнение
2k^2 - k - 1 = 0
(k - 1)(2k + 1) = 0
k1 = 1; k2 = -1/2
Решение однородного уравнения:
y0 = C1*e^x + C2*e^(-x/2)
Теперь решаем неоднородное уравнение.
Правая часть f(x) = e^x + sin x
Неоднородная часть решения:
y* = Axe^x + Bsin x + Ccos x
y* ' = Ae^x + Axe^x + Bcos x - Csin x
y* '' = Ae^x + Ae^x + Axe^x - Bsin x - Ccos x = 2Ae^x + Axe^x - Bsin x - Ccos x
Подставляем в уравнение
2(2Ae^x + Axe^x - Bsin x - Ccos x) - (Ae^x + Axe^x + Bcos x - Csin x) -
- (Axe^x + Bsin x + Ccos x) = e^x + sin x
4Ae^x + 2Axe^x - 2Bsin x - 2Ccos x - Ae^x - Axe^x - Bcos x + Csin x -
- Axe^x - Bsin x - Ccos x = e^x + sin x
e^x*(4A-A) + xe^x*(2A-A-A) + sin x*(-2B+C-B) + cos x*(-2C-B-C) = e^x + sin x
3A*e^x + 0*xe^x + (-3B+C)*sin x + (-B-3C)*cos x = e^x + sin x
Составляем систему:
{ 3A = 1
{ -3B + C = 1
{ -B - 3C = 0
Решаем:
{ A = 1/3
{ -9B + 3C = 3
{ -B - 3C = 0
Получаем:
{ A = 1/3
{ B = -3/10 = -0,3
{ C = -B/3 = 1/10 = 0,1
Неоднородная часть решения:
y* = Axe^x + Bsin x + Ccos x = x/3*e^x - 0,3sin x + 0,1cos x
Полное решение:
y = y0 + y* = C1*e^x + C2*e^(-x/2) + x/3*e^x - 0,3sin x + 0,1cos x