Пошаговое объяснение:
Среднее арифметическое это частное от деления суммы чисел на число слагаемых.
Медиана нечетного количества чисел – это число, записанное посередине.
Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Размах ряда чисел – это разница между наибольшим числом и наименьшим .
1) Упорядочим ряд из 6 чисел
3; 4; 6; 7; 7; 9
Среднее арифметическое
(3+4+6+7+7+9)/6=36:6=6
Медиана
поскольку ряд чисел четный , то медиана будет
(6+7)/2=13/2=6,5
Размах ряда
9-3=6
2) Упорядочим ряд из 5 чисел
1,9; 2,7; 3,8; 4,2; 5,9
Среднее арифметическое
(1,9+ 2,7+ 3,8+ 4,2+ 5,9)/5=18,5/5=3,7
Медиана
поскольку ряд чисел нечетный , то медиана будет
3,8
Размах ряда
5,9 - 1,9 =4
3) Упорядочим ряд из 5 чисел
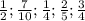
поскольку у нас дробные числа , приведем их к одному знаменателю
10=2*5
4=2*2
5- простое число
НОК (2;4;5;10)=2*2*5=20
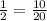
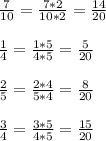
Теперь упорядочим ряд с одинаковыми знаменателями
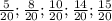
значит наш ряд будет
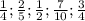
Среднее арифметическое
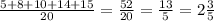
Медиана
поскольку ряд нечетный то медиана будет
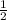
Размах ряда
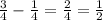

также скобки в ответе могут быть либо квадратные [], либо круглые (), может встретиться смесь и круглых скобок с квадратными [) или
(]
1.
{2x+7≥1
{x-3<1
переносим неизвестные в одну сторону, а известные в другую. не забывай менять знаки:
{2x≥1-7
{x<1+3
считаем:
{2x≥-6
{x<4
делишь правую часть на неизвестный коэффициент:
{x≥-3
{x<4
рисуем числовой промежуток:
[-3](4)
отмечаем промежутки:
[-3](4)
направление этих "палочек" зависит от знака данного в системе. например, если знак такой x<4, то отмечаем "палочки" в левую сторону, так как знак показывает, что x меньше 4-ех, поэтому от 4-ех рисуем "травку" в меньшую сторону.
место пересечения промежутков и есть ответ
ответ: [-3;4)
2.
{3y<21
{4-y>0
работаем по той же схеме:
{y<7
{-y>-4
в неравенстве где y отрицателен меняем знак (знак будет меняться, если неизвестный коэффициент отрицательный):
{y<7
{y<4
(4)(7)
возьмем неравенство со знаком y<7, то есть это значит, что y меньше 7-ми, поэтому от 7-ми рисуем "травку" влево, где находятся числа меньше 7-ми
ответ:(-∞;4)
3.
{4x+9>-15
{2-x≤5
{4x>-15-9
{-x≤5-2
{4x>-24
{-x≤3
{x>-6
{x≥-3
во втором неравенстве поменяли знак, так как х был отрицателен
(-6)[-3]
ответ:[-3;+∞)