Question

(x^2-a(a+1)x+a^3)/√(2+x-x^2)=0
когда уравнение имеет 2 разных корня

Answer 1

Решение: Запишем ОДЗ: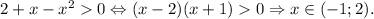 $2+x-x^2 0\Leftrightarrow (x-2)(x+1) 0\Rightarrow x\in(-1; 2).$

Переходим к уравнению-следствию: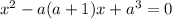 $x^2-a(a+1)x+a^3=0$.  

Найдём дискриминант:  $D=[-a(a+1)]^2-4\cdot1\cdot a^3=a^4+2a^3+a^2-4a^3=a^4-2a^3+a^2=a^2(a^2-2a+1)=a^2(a-1)^2=[a(a-1)]^2.$

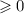Дискриминант $\geqslant 0$ при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При 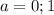$a = 0; 1$ дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все 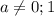$a\neq0;1$. Для них квадратное уравнение имеет два корня:

$x_1=\frac{a(a+1)-a(a-1)}{2}= \frac{2a}{2}=a;\\\\x_2= \frac{a(a+1)+a(a-1)}{2}= \frac{2a^2}{2}=a^2.$

Чтобы исходное уравнение имело два корня необходимо, чтобы оба корня удовлетворяли ОДЗ, т.е.

$\left \{ {{-1< a$

Не забудем исключить 0 и 1 из данного промежутка значений и получим окончательный ответ.

ОТВЕТ: при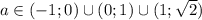 $a\in(-1; 0)\cup(0; 1)\cup(1;\sqrt2)$.