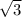,но с решением !
Диагональ прямоугольника разбивает его на два равных прямоугольных треугольника .
В этих треугольниках диагональ является гипотенузой, а катеты - это длина и ширина исходного прямоугольника .
Применим теорему Пифагора .
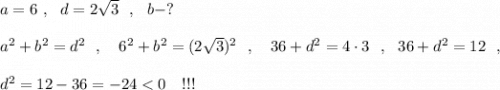
Квадрат диагонали не может получится отрицательным ⇒ в условии допущена ошибка .
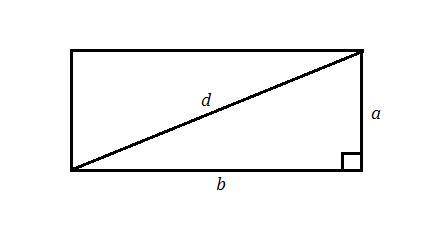
Уравнение \sin x=a при |a|>1 решений не имеет,
при a=1 имеет решения \displaystyle x=\frac{\pi}{2}+2\pi k,\ k\in\mathbb{Z},
при a=-1 имеет решения \displaystyle x=\frac{3\pi}{2}+2\pi k,\ k\in\mathbb{Z},
при a=0 имеет решения x=\pi k,\ k\in\mathbb{Z},
при всех остальных a имеет решения x=(-1)^k{\rm arcsin}\,a+\pi k, k\in\mathbb{Z}.
Уравнение \cos x=a при |a|>1 решений не имеет,
при a=1 имеет решения x=2\pi k,\ k\in\mathbb{Z},
при a=-1 имеет решения x=\pi+2\pi k,\ k\in\mathbb{Z}>,
при a=0 имеет решения \displaystyle x=\frac{\pi}{2}+\pi k,\ k\in\mathbb{Z},
при всех остальных a имеет решения x=\pm{\rm arccos}\,x+2\pi k, k\in\mathbb{Z}.
Уравнение {\rm tg}\, x=a имеет решения x={\rm arctg}\, x+\pi k,\ k\in\mathbb{Z}.
Уравнение {\rm ctg}\, x=a имеет решения x={\rm arcctg}\, x+\pi k,\ k\in\mathbb{Z}.
Пошаговое объяснение:
(см. объяснение)
Пошаговое объяснение:
Так как диагональ лежит против прямого угла, то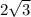
должна быть наибольшей стороной треугольника. Однако 
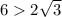, поэтому такого прямоугольника не существует.
Задание выполнено!
Комментарий:
Можно было решать задачу иначе. Прямоугольник существует только, если выполняется равенство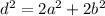
, где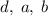 
- это диагональ и боковые стороны соответственно. Выполним подстановку данных из условия: 
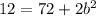. Получили аналогичный результат.