Здесь за одно и то-же время было два движения:
1. Фляга со скоростью течения реки (обозначим X) проплыла от первого моста (момент потери) до воторого (пловец ее догнал) 1км. Т.о. можно вычислить время за которое это проихошло как: 1/X ч.
2. Пловец вначале 10 минут (10/60=1/6) или 1/6 часа плыл против течения со скоростью Y-X, где Y - собственная скорость пловца в стоячей воде). За это время он проплыл расстояние (1/6)*(Y-X). Потом он повернул обратно и за оставшееся время проплыл путь длиной 1+(1/6)*(Y-X) со скоростью Y+X (т.к. он плыл уже по течению). Это оставшееся время можно найти как (1+(1/6)*(Y-X))/(Y+X).
Все это можно совместить следущим образом:
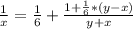
Осталось найти из этого X:
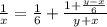
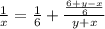
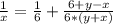
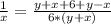
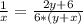
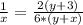
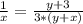
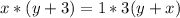
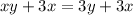
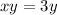
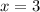
ОТВЕТ 3 км/ч
Для решения применим алгоритм Евклида.
Ключевая идея заключается в том, что НОД чисел a и b (a < b) равен НОД числа a и остатка при делении b на a.Как не сложно убедиться, 5n - 4 делится на n - 1 с остатком 1.
5n - 4 = 5 (n - 1) + 1
Следовательно, в записи НОД мы можем 5n - 4 заменить на 1:
НОД (n - 1; 5n - 4) = НОД (n - 1; 1) = 1
Задача решена!
ответ: 1