
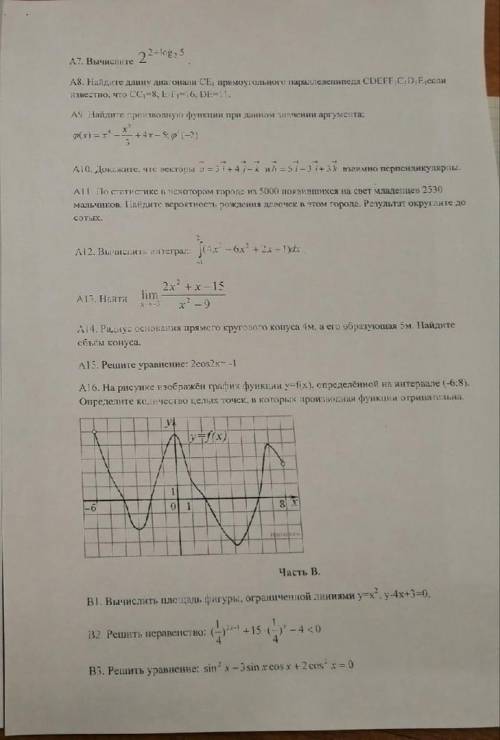
Уравнение прямой 2х – 3у = 6 преобразуем в уравнение с угловым коэффициентом: у = (2х – 6)/3 = (2/3)х - 0,5.
Находим точку С на оси Оу (при этом х = 0): С(0; -0,5).
Разность координат при параллельном переносе:
Δх = 1 - (-1) = 2.
Δу = -1 - 1= -2.
Точка С (0; -0,5) на прямой перейдёт в точку:
Д(0 + 2 = 2; -0,5 + (-2) = -2,5) = (2; -2,5).
Угловой коэффициент её сохранится и уравнение примет вид:
у = (2/3)х + в. Для определения параметра в подставим координаты точки Д(2; -2,5).
-2,5 = (2/3)*2 + в,
в = (-5/2) - (4/3) = -23/6.
ответ: у = (2/3)х - (23/6) или 4х - 6у - 23 = 0.
возведем оба уравнения в квадрат
(2√x-√y)²=3²
(√x√y)²=2²
4x-4√x√y+y=9 √x√y=2 по условию задачи
xy=4
4x-8+y=9
xy=4
4x+y=17
xy=4
тут можно методом подбора понять что x=4 а y=1
а если метод подбора неубедителен то надо из первого уравнения выразить y через х и подставить во второе уравнение получится квадратное уравнение
y=17-4x
x(17-4x)=4
17x-4x²=4, 4x²-17x+4=0 , x1-2=(17+-√289-64)/8=(17+-15)/8
x1=4, x2=1/4
y1=17-16=1 y2=17-1=16
1) первое решение x=4, y=1
2) второе решение не подходит так как не обращает в верное равенство первое уравнение, так иногда бывает при возведении в квадрат