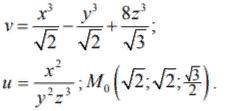
Пошаговое объяснение:
1)площадь равных фигур равны - верно
2)если равны площади фигур,то равны и фигуры - неверно
3)периметры равны прямоугольнику равны -верно
4)если периметры прямоугольников равны,то равны и прямоугольники - неверно
5)если площади прямоугольников равны, то равны и прямоугольники -неверно
6)площадь прямоугольника равна произведению его длин и ширины -верно
7)площадь квадрата равна квадрату его стороны -верно
8)площадь всех фигур равна сумме площадей её частей - верно
9)если периметры квадратов равны, то равны и их площади -верно
ответ : 136789
Пошаговое объяснение:
1)площадь равных фигур равны - верно
2)если равны площади фигур,то равны и фигуры - неверно
3)периметры равны прямоугольнику равны -верно
4)если периметры прямоугольников равны,то равны и прямоугольники - неверно
5)если площади прямоугольников равны, то равны и прямоугольники -неверно
6)площадь прямоугольника равна произведению его длин и ширины -верно
7)площадь квадрата равна квадрату его стороны -верно
8)площадь всех фигур равна сумме площадей её частей - верно
9)если периметры квадратов равны, то равны и их площади -верно
ответ : 136789
ОТВЕТ: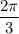 , или
, или 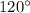 .
.
Объяснение: Найдем частные производные 1-го порядка функции :
:
Градиент функции :
:
Аналогичным образом находим градиент функции в точке
в точке 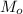 :
:
По определению скалярного произведения:
Модули градиентов:
Скалярное произведение градиентов:
Косинус искомого угла:
Отсюда искомый угол: