Пошаговое объяснение:
Решение дано на фото.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
Пошаговое объяснение:
1.
Пусть Анар соберет помидоры за х минут, тогда
за 1 минуту он соберет 1/х часть помидоров
за 1 минуту Жанар соберет 1/18 часть помидоров
за 1 минуту они вдвоем соберут 1/15 часть помидоров
1/х + 1/18 = 1/15
270+15х=18х
3х=270
х=90.
ответ: за 90 минут.
2.
Пусть вторая группа выполнит работу за х часов, тогда
за 1 час она выполнит 1/х часть работы
первая группа за 1 час выполнит 1/15 часть работы
две группы вместе за 1 час выполнят 1/6 часть работы
1/х + 1/15 = 1/6
30+2х=5х
3х=30
х=10
ответ: за 10 часов
3.
Пусть Арай выполнит заказ за х часов, тогда
за 1 час она выполнит 1/х часть заказа
за 1 час Сауле выполнит 1/12 часть заказа
за 1 час они выполнят 1/8 часть заказа
1/х + 1/12 = 1/8
24+2х=3х
х=24.
ответ: за 24 часа
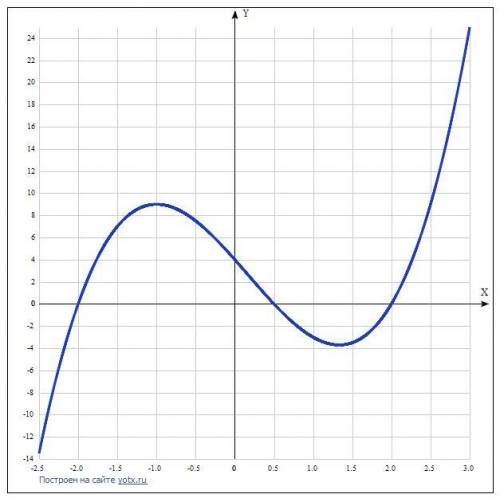
Дана функция f(x)=2x^3-x^2-8x+4.
) Область определения функции D.
Так нет ограничений, то D ∈ (-∞; +∞).
2) Особые свойства функции - особых нет.
3) Нахождение точек пересечения графика с осями.
Если х = 0, то точка пересечения с осью Оу = 4.
Если у = 0, то надо решить кубическое уравнение:
2x^3-x^2-8x+4 = 0.
Иногда удаётся найти корни уравнения среди множителей свободгого члена: +-1, +-2, +-4.
В данном уравнении подходят корни х = +-2.
Разделив последовательно заданное выражение на (х - 2) и (х + 2), находим третий корень х = 0,5.
4) Нахождение промежутков монотонности.
Находим производную функции.
y' = 6x² - 2x - 8 и приравниваем её нулю.
6x² - 2x - 8 = 0 или 3x² - x - 4 = 0. D = 1 - 4*3*(-4) = 49. √D = +-7.
x1 = (1 - 7) / 6 = -1,
x2 (1 + 7)/6 = 8/6 = 4/3.
Это критические точки, в которых производная равна нулю.
Нахождение локального экстремума.
Определяем характер найденных критических точек по знакам производной левее и правее этих точек.
х = -2 -1 0 4/3 2
y' = 20 0 -8 0 12.
Максимум в точке х = -1, у = 9,
минимум в точкех = 4/3, у = -100/27.
Из этой таблицы получаем и свойство функции на промежутках.
Получено 3 промежутка монотонности:
(-∞; -1) и ((4/3; +∞) функция возрастает,
(-1; (4/3)) функция убывает.
5) Нахождение интервалов выпуклости графика функции.
Находим вторую производную функции.
y'' = 12x - 2. Приравниваем её нулю:12х - 2 = 0 или 6х - 1 = 0.
Отсюда получаем одну точку перегиба функции х = 1/6.
(-∞; (1/6)) выпуклость вверх,
((1/6); +∞) выпуклость вниз (по знакам второй производной).