Відповідь:
Схема и решение прилагаются.
Покрокове пояснення:
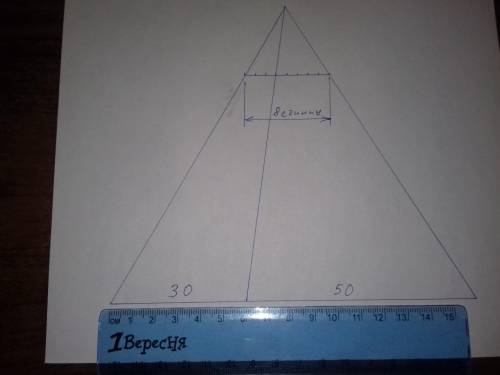
В качестве бонуса графический решения задачи ( без вычисления ).
Чертится линия состоящая из двух отрезков 30 и 50 единиц. Затем от точек отрезков проводятся три линии сходящиеся в одну точку ( вершина треугольника ). После этого проводится отрезок желательно параллельный основанию треугольника ( но не обязательно ), длина отрезка равна 8 единицам ( при этом единицы на проводимом отрезке и в основании пирамиды могут быть разными ( нам главное пропорция ). Я взял отрезок длиной в 8 тетрадных клеток.
В результате верхний отрезок разделится на два по 3 и по 5 клеток - это и есть искомые цены.
Пусть имеется
чисел. Мы знаем, что, в частности, сумма всех чисел не делится на 3. Если эта сумма дает остаток 1 при делении на 3, то сумма первых 
чисел делится на 3, что невозможно. Значит, сумма всех чисел дает остаток 2 от деления на 3. Если любое некрайнее число увеличить на 1, то сумма всех чисел будет делиться на 3 и свойство нарушится. Если же любое некрайнее число уменьшить на 1, то сумма первых 
чисел делится на 3, поскольку давала остаток 1.