действуем по алгоритму нахождения наименьшего значения функции на отрезке:
Область определения функции не ограничена: D(y) = R.Производная функции равна: y’ = 3x2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.Нули производной: y’ = 3x2 – 36x + 81 = 0, значит x2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x3 – 18x2 + 81x + 23 = x(x-9)2+23: y(8) = 8 · (8-9)2+23 = 31;y(9) = 9 · (9-9)2+23 = 23;y(13) = 13 · (13-9)2+23 = 231.Итак, из полученных значений наименьшим является 23. ответ: 23.
(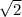 /10 ; -7
/10 ; -7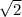 /10 )
/10 )
Пошаговое объяснение:
Координаты основания медианы это полусумма координат стороны на которой оно лежит. Т.е. ( (3+9)/2 ; (6+4)/2 ) = (6;5)
Вектор медианы BD получается как разность координат точек D и B.
Тогда он равен (6-5;5-12) = (1;-7)
Для получения единичного вектора надо полученный вектор разделить на его длину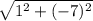 = 5
= 5 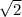
Тогда единичный вектор равен ( 1/(5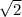 ) ; -7/(5
) ; -7/(5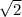 ) )
) )
или (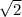 /10 ; -7
/10 ; -7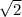 /10 )
/10 )
такой ответ если в условии нет ошибки