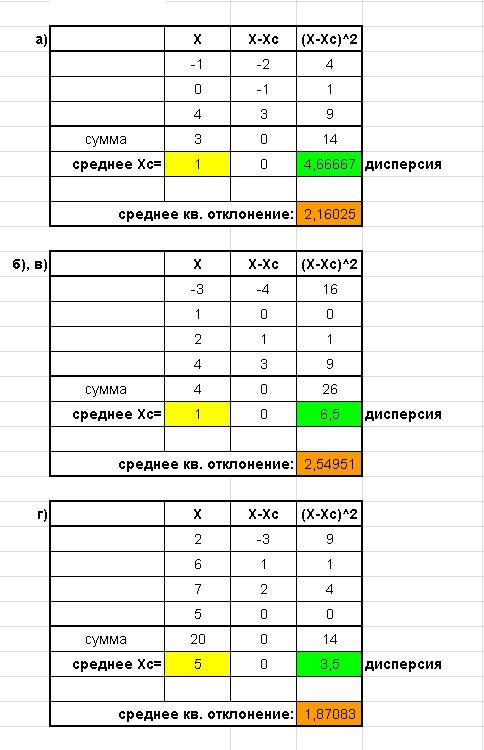
Картинка с табличками вложена. Искомые величины выделены цветом.
а)
Сначала находим среднее значение выборки:
Хс = (-1 + 0 + 4)/3 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n}} = \\
\sqrt{\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 2,1602
Дисперсия - это средний квадрате отклонений от средней величины:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n} = \\
\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 4,6667
б)
Среднее значение выборки:
Хс = (-3 + 1 + 2 + 4)/4 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 2,5495
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} = \\
\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 6,5
в) смотри б)
г)
Среднее значение выборки:
Хс = (2 + 6 + 7 + 5)/4 = 5
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 1,8708
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} =
\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 3,5
Решение
1) 12 : 100 = 0,15 (см) 1% от длины первой стороны;
2) 0,15 * 80 = 12 (см) длина второй стороны;
3) 12 : 100 = 0,12 (см) 1% от длины второй стороны;
4) 0,12 * 150 = 18 см (см) длина третьей стороны.
5) 12 + 15 + 18 = 45 (см).
ответ: периметр треугольника равен 45 см
Пошаговое объяснение:
Решение
1) 12 : 100 = 0,15 (см) 1% от длины первой стороны;
2) 0,15 * 80 = 12 (см) длина второй стороны;
3) 12 : 100 = 0,12 (см) 1% от длины второй стороны;
4) 0,12 * 150 = 18 см (см) длина третьей стороны.
5) 12 + 15 + 18 = 45 (см).
ответ: периметр треугольника равен 45 см
Пошаговое объяснение:
а)(2 3/7+5 4/7)-3 7/9=8-3 7/9=4 2/9
б)(13.24-4.34)÷4+7.775=8.9÷4+7.775=89/40+7 775/1000=2 9/40+7 31/40=10
ба:
в)5.24×2.743+4.76×2.743=2.743(5.24+4.76)=2.743×10=27.43