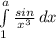 . Вместо а - ∞. ответ: сходится
. Вместо а - ∞. ответ: сходитсяРазложим на простые множители 72
72 = 2 • 2 • 2 • 3 • 3
Разложим на простые множители 120
120 = 2 • 2 • 2 • 3 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (72; 120) = 2 • 2 • 2 • 3 = 24
792=2*2*2*3*3*11
1188=2*2*3*3*3*11
НОД (792;1188) = 2*2*3*3*11=396
НОК (792;1188) = 2*2*2*3*3*11*3=2376
Разложим на простые множители 396
396 = 2 • 2 • 3 • 3 • 11
Разложим на простые множители 924
924 = 2 • 2 • 3 • 7 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 3 , 11
Находим произведение одинаковых простых множителей и записываем ответ
НОД (396; 924) = 2 • 2 • 3 • 11 = 132
НОД (116;111) = 1
111 = 3×37
116 = 2×2×29
Подробнее - на -
Разложим на простые множители 72
72 = 2 • 2 • 2 • 3 • 3
Разложим на простые множители 120
120 = 2 • 2 • 2 • 3 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (72; 120) = 2 • 2 • 2 • 3 = 24
792=2*2*2*3*3*11
1188=2*2*3*3*3*11
НОД (792;1188) = 2*2*3*3*11=396
НОК (792;1188) = 2*2*2*3*3*11*3=2376
Разложим на простые множители 396
396 = 2 • 2 • 3 • 3 • 11
Разложим на простые множители 924
924 = 2 • 2 • 3 • 7 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 3 , 11
Находим произведение одинаковых простых множителей и записываем ответ
НОД (396; 924) = 2 • 2 • 3 • 11 = 132
НОД (116;111) = 1
111 = 3×37
116 = 2×2×29
Подробнее - на -
Сходится
Пошаговое объяснение:
Особая точка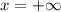 .
.
Подынтегральная функция представима в виде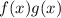 , где
, где 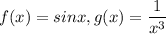 .
.
1)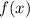 непрерывна на
непрерывна на 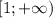 .
.
2)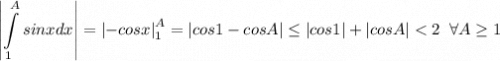
3)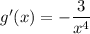 непрерывна на
непрерывна на 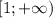 . При этом
. При этом 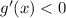 , а значит
, а значит 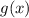 монотонно убывает.
монотонно убывает.
4)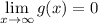
Значит, интеграл сходится по признаку Дирихле.