1. Сумма углов треугольника равна 180°. Один из его углов равен 90°, тогда сумма двух оставшихся острых равна 180° - 90° = 90°.
Именно поэтому для нахождения второго острого угла достаточно из 90° вычесть величину первого острого угла.
В нашем случае
90° - 36° = 54° - величина второго острого угла прямоугольного треугольника.
2. 36° : 180° = 36/180 = 1/5 = 0,2 = 20% суммы всех углов составляет величина первого острого угла.
3. 54° : 180° = 54/180 = 3/10 = 30% суммы всех углов составляет величина второго острого угла.
Величина второго острого угла - 54°. Сумма углов треугольника - 180°. Острый угол величиной 36° составляет 20% от суммы углов треугольника, а второй острый угол 54° – 30%.
1. 15
2. 45
Пошаговое объяснение:
1. Поскольку в условии задачи сказано, что трактористы (и первый, и второй) вспахали такую-то часть от всей земли, чтобы узнать, сколько га вспахал третий, мы можем сложить части вспаханной земли каждого тракториста. Это можно делать, чтобы найти то, чего не хватает, то есть часть третьего тракториста, только если в условии сказано, что рабочие вспахали часть от всей земли. Если же условие звучит, как в третьей задаче, нужно действовать иначе. Это очень важно.
1) Складываю части вспаханной земли первого и второго тр-та., получаю 20/21.
Если бы трактористы были одним человеком, это было бы частью от всей земли, которую он вспахал.
Чтобы найти, сколько вспахал третий, нужно вычесть из целого - у дробей целое - единица - эту дробь.
2) ответ 1/21.
3) Нужно узнать, сколько в га вспахал третий тракторист. У нас есть дробь, показывающая, сколько от всей земли он вспахал - одну двадцать первую часть.
Великая истина - чтобы найти дробь ОТ числа, нужно умножить число на дробь (или наоборот, дробь на число, ведь это - умножение, и от смены мест множителей ничего не меняется),
а чтобы найти какую часть от числа СОСТАВЛЯЕТ дробь, нужно (внимание! именно число на дробь, не наоборот) разделитьчисло на дробь. Так же иногда используется формулировка, пример: "число ЭТО такая-то часть".
Таким образом, ОТ = всегда умножение, "СОСТАВЛЯЕТ", "ЭТО" = всегда деление числа на часть (дробь).
3) Умножаем, раз нам нужно найти дробь ОТ числа.
ответ: 15 га.
2. Во второй день в этой задаче продали 7/15 от того, ЧТО ОСТАЛОСЬ В ПЕРВЫЙ ДЕНЬ. То есть, остаток в первый день становится целым для второго дня. Поэтому мы не можем просто сложить данные условием дроби, вычесть это из единицы и найти в килограммах сколько продано в третий день.
1) Считаем, сколько продано в первый день в кг. Умножаем дробь на число.
2) Очень важно! Находим остаток масла после первого дня, вычитая из целого проданное. 120 - 45.
3) В условии написано так: "за второй [день продано] 7/15 остатка." Находим 7/15 от остатка в 75 кг.
4) Теперь в килограммах находим, сколько продано в третий день.
ответ: 45


(см. объяснение)
Пошаговое объяснение:
В своем ответе приведу три составленные задачи:
Задача №1:
На доске написано натуральное четырехзначное число. Известно, что при делении этого числа на сумму его цифр получалось число 71. Определите это число.
ответ: было записано число 1278.
Задача №2:
На доске написано три трехзначных натуральных числа. Известно, что сумма цифр каждого не превышает 9. Была найдена сумма цифр каждого числа (под каждым исходным числом на доске записали соответствующее однозначное число). Найденные числа расположили друг за другом в порядке возрастания без промежутков так, что получилось новое трехзначное число. Возможно ли, что при делении суммы трех исходных трехзначных чисел на полученное трехзначное число получится целое число X, причем наибольшее из трех исходных чисел должно делиться на наименьшее из них без остатка так, чтобы в результате такого деления получалось число X-1.
ответ: да, возможно, например, это числа 100, 210, 500.
Задача №3:
Было загадано три различных натуральных двузначных числа: a, b и c. Может ли следующее равенство быть верным: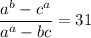 .
.
ответ: да, например, при a=31, b=32, c=10.
Задание выполнено!