
Самое полезное для меня "открытие" - это прямоугольный "египетский" треугольник.
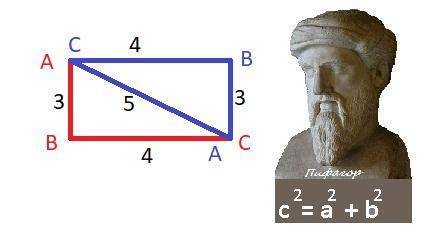
Это треугольник со сторонами 3:4:5.
Нужно было разметить фундамент для теплицы - прямоугольник.
Вот с верёвки я (мы) сделали разметку.
Взяли верёвку длиной = 3+4+5 = 12 метров, завязали узлы в нужных точках и растянули образовав треугольник. Забили по углам колышки, и проверили разметку с другой стороны. Получили четвёртую точку.
А затеи проверили прямой угол, измерив диагонали - они должны быть равными - по 5 метров. Оказалось всё точно предку - Пифагору - в приложении.
у= ∛х
х=26,46
У=∛26,46
когда вычисление квадратного корня столбиком нам по плечу, почему бы не взяться за задачу следующего ранга – вычисление столбиком корня кубического? Народная молва не зря давненько обходит стороной всю эту кубистику, непроста ведь аналитическое решение кубических уравнений хоть и существует, но никто не хочет с ним связываться. Но мы - не лыком шиты, прорвемся.
А для начала пойдем уже проторенным путем, вспомним формулу куба двухчлена: (a+b)**3= a**3+ 3*a*2*b+ 3*a*b*2+ b**3= a**3+ b*(3*a**2+ 3*a*b+ b**2)= a*3+ b*(3*a(a+ b)+ b**2). Поскольку речь идет о вычислених в 10-ичой СС, заменим теперь a на 10*a, и получим (10*a+b)**3= 1000*a**3+ b*(30*a*(10*a+b)+ b**2), откуда 10*a+b=(1000*a**3+ b*(30*a*(10*a+b)+ b**2))**(1/3)=> a+ b/10= (a**3+ b*(30*a*(10*a+ b)+ b**2)/1000))**(1/3). Таким образом, как уже понятно, дело сводится к целочисленному, с остатком, решению необычного уравнения: b*(30*a*(10*a+ b)+ b**2)= 1000. То есть нужно выполнить следующее целочисленное деление b= 1000/(30*a*(10*a+ b)+ b**2). Какова практическая механика решения?
(Оговорка: если корень извлекался, например, из 26,46 , то данное уравнение следовало бы изменить на 2646/(30*12*(120+b)+b**2). И так же на других шагах: последний остаток умножать на 100 и прибавлять следующую тройку цифр из подкоренного числа.)
решив уравнение мы получим приблизительно 2.963
Вопрос про бесконечность минус бесконечность очень важный. Если Вам дан обычный определенный (собственный) интеграл (интеграл Римана), функция обязана быть ограниченной (хотя этого может и не хватить для существования интеграла). Поэтому ни о какой бесконечности речи быть не может. Если интеграл понимается как несобственный, функция может быть и неограниченной, но если при вычислении предела от первообразной где-то получится бесконечность, интеграл сразу признается расходящимся. Но бывает еще интеграл в смысле главного значения - вот там бесконечности могут скушать друг друга.
Пример.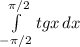 . Как собственный интеграл он не существует (не существует конечный предел интегральных сумм, не зависящий от разбиения и выбора промежуточных точек), как несобственный интеграл он расходится, а в смысле главного значения равен нулю.
. Как собственный интеграл он не существует (не существует конечный предел интегральных сумм, не зависящий от разбиения и выбора промежуточных точек), как несобственный интеграл он расходится, а в смысле главного значения равен нулю.