
Пошаговое объяснение:
у=х⁴-4х³-8х²+12
1) Область определения функции.
D(f) = R
2) Находим производную функции.
у' = 4х³-12х²-16х
3)Найдем нули производной:
y' = 0;
4х³-12х²-16х=0
4х(х²-3х-4)=0,
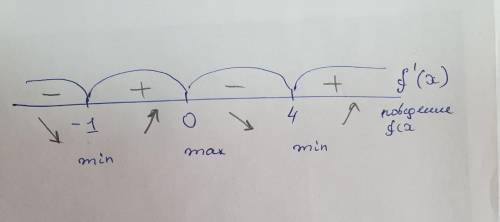
х₁=0, х₂=4 , х₃=-1 - критические точки (точки экстремума)
4) Получилось четыре промежутка:
(-∞; -1), (-1;0), (0; 4) и (4; +∞).
5) Расставим знаки производной на каждом промежутке:
(-∞; -1) если х = -2: y'(-2) = -8(4+6-4)= <0 (минус).
(-1;0) если х = 1: y'(-0,5) = -2(0,25+1,5-4) = 4,5 >0 (плюс).
(0; 4) если х = 1: y'(1) = 4(1-3-4) <0 (минус).
(4; +∞) если х = 5: y'(5) = 20(25-15-4) >0 (плюс).
6)Определяем промежутки возрастания и убывания функции
Если знак производной функции на промежутке положительный, то функция возрастает, если отрицательный - то убывает.
Функция возрастает (производная плюс) на х∈ (-1;0), (4;+∞)
Функция убывает на х∈ (-∞; -1) и (0;4;)
точка минимума функции х=-1; 4; точка максимума функции х=0.
f(x) max = f(0) = 12, минимум (0;12)
f(x) min =f(-1) = (-1)⁴-4*(-1)³-8*(-1)²+12 = 1+4-8+12=9
f(x) min =f(4) = (4)⁴-4*(4)³-8*(4)²+12=256-256-128+12=116
максимум (-1;9), (4; -116)
Пошаговое объяснение:
у=х⁴-4х³-8х²+12
1) Область определения функции.
D(f) = R
2) Находим производную функции.
у' = 4х³-12х²-16х
3)Найдем нули производной:
y' = 0;
4х³-12х²-16х=0
4х(х²-3х-4)=0,
х₁=0, х₂=4 , х₃=-1 - критические точки (точки экстремума)
4) Получилось четыре промежутка:
(-∞; -1), (-1;0), (0; 4) и (4; +∞).
5) Расставим знаки производной на каждом промежутке:
(-∞; -1) если х = -2: y'(-2) = -8(4+6-4)= <0 (минус).
(-1;0) если х = 1: y'(-0,5) = -2(0,25+1,5-4) = 4,5 >0 (плюс).
(0; 4) если х = 1: y'(1) = 4(1-3-4) <0 (минус).
(4; +∞) если х = 5: y'(5) = 20(25-15-4) >0 (плюс).
6)Определяем промежутки возрастания и убывания функции
Если знак производной функции на промежутке положительный, то функция возрастает, если отрицательный - то убывает.
Функция возрастает (производная плюс) на х∈ (-1;0), (4;+∞)
Функция убывает на х∈ (-∞; -1) и (0;4;)
точка минимума функции х=-1; 4; точка максимума функции х=0.
f(x) max = f(0) = 12, минимум (0;12)
f(x) min =f(-1) = (-1)⁴-4*(-1)³-8*(-1)²+12 = 1+4-8+12=9
f(x) min =f(4) = (4)⁴-4*(4)³-8*(4)²+12=256-256-128+12=116
максимум (-1;9), (4; -116)

(см. объяснение)
Пошаговое объяснение:
Рассмотрим сначала первое неравенство системы:
Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если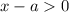 .
.
Тогда при домножении левой и правой частей неравенства на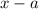 его знак сохранится.
его знак сохранится.
Получим эквивалентную систему:
Преобразуем ее до более удобного вида:
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
Преобразуем ее:
Приведем систему к более удобному виду:
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
Откуда следует, что при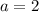 исходная система неравенств имеет единственное решение
исходная система неравенств имеет единственное решение 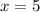 .
.
Задание выполнено!