ответ: №4 .
Геометрическим местом точек, равноудалённых от концов отрезка АВ, является серединный перпендикуляр 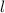 этого отрезка , проходящий через точку М .
этого отрезка , проходящий через точку М .
 и
и  а уравнение всего одно:
а уравнение всего одно:  то решений может быть бесконечно много.
то решений может быть бесконечно много.
 а значит:
а значит: 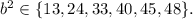
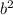 – не является квадратом натурального числа, а значит, целых решений нет.
– не является квадратом натурального числа, а значит, целых решений нет.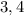 и
и  и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы  этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник больше и относится к упомянутому египетскому, как
Ясно, что наш треугольник больше и относится к упомянутому египетскому, как  т.е. больше него в
т.е. больше него в 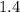 раза, соответственно и катеты больше в
раза, соответственно и катеты больше в 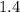 раза, т.е. вместо катетов
раза, т.е. вместо катетов 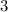 и
и 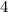 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты 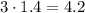 и
и 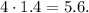
 и
и 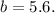
 ;
;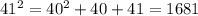 ;
;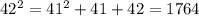 ;
; ;
; ;
;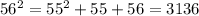 ;
; ;
;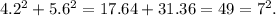
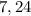 и
и  и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы  этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как
Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как 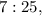 т.е. составляет от него часть:
т.е. составляет от него часть: 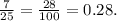 Соответственно и катеты меньше, т.е. вместо катетов
Соответственно и катеты меньше, т.е. вместо катетов  и
и 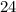 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты 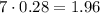 и
и 
 и
и 
 и
и 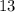 и рассчитать катеты из подобия гипотенузы
и рассчитать катеты из подобия гипотенузы 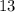 этого треугольника и нашего исходного треугольника с гипотенузой
этого треугольника и нашего исходного треугольника с гипотенузой  Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как
Ясно, что наш треугольник меньше и относится к упомянутому египетскому, как  т.е. составляет от него часть:
т.е. составляет от него часть: 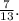 Соответственно и катеты меньше, т.е. вместо катетов
Соответственно и катеты меньше, т.е. вместо катетов  и
и 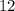 исходного египетского нужно брать катеты
исходного египетского нужно брать катеты  и
и 
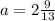 и
и 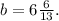
 и
и 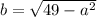
 и
и 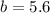 ;
; и
и 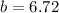 ;
;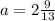 и
и 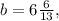 кроме которых существует бесконечное число аналогичных рациональных решений.
кроме которых существует бесконечное число аналогичных рациональных решений.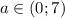 и
и 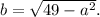
Пошаговое объяснение:
Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).
Решать задачу будем следующим образом:
вспомним формулу для нахождения расстояния между точками на плоскости;
обозначим точки равноудаленные от А и В координатами (x; y);
запишем расстояния между точкой А и (x; y);
запишем расстояние между точками B и (x; y);
приравняем расстояния и выразим одну переменную через другую.
Вспомним формулу для нахождения расстояния на плоскости
Формула для нахождения расстояния между точками на плоскости выглядит так:
AB =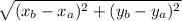 , где точки А и В заданы координатами A и B
, где точки А и В заданы координатами A и B
Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).
Составим уравнение геометрического места точек
Записываем расстояние между точкой A (2; -3) и (x; y):
Записываем расстояние между точками B (-4; 1) и (x; y):
Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:
Открываем скобки, переносим все слагаемые в право и приводим подобные.
или